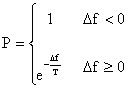Annealed Demon Algorithms Solving the Environmental / Economic Dispatch Problem
Aristidis VLACHOS* and Evangelos TSANOS
Department of Informatics, Univercity of
E-mails: Aris532003@yahoo.gr, v_tsanos@yahoo.com
* Corresponding author: Phone: +30 6937 480 570
Abstract
This paper presents an efficient and reliable Annealed Demon (AD) algorithm for the Environmental/Economic Dispatch (EEB) problem. The EED problem is a multi-objective non-linear optimization problem with constraints. This problem is one of the fundamentals issues in power system operation. The system of generation associates thermal generators and emissions which involves sulphur oxides (SO2) and nitrogen oxides (NOx). The aim is to minimize total fuel cost of the system and control emission. The proposed AD algorithm is applied for EED of a simple power system.
Keywords
Environmental/Economic Dispatch (EED) Problem; Simulated Annealing (SA) Algorithm; Demon Algorithm.
Introduction
In electric power plants, Economic Dispatch (ED) is used to minimize fuel costs while satisfying all thermal generators and System equality and inequality constraints [1].
The generation of electricity from the fossil fuel releases contaminants, mainly sulphur oxides (SO2) and nitrogen oxides (NOx), into the atmosphere. As a result, EED problem has been proposed in the area of generation dispatch, which simultaneously minimizes both fuel cost and pollutant emissions [2,3].
Different techniques and heuristic methods have been proposed to handle this problem including particle swarm optimization (PSO) [4-6], evolutionary algorithms [7,8], fuzzy satisfaction-maximizing decision approach [9], genetic algorithm (GA) [10], artificial immune system [11] and hybrid methods [12-14].
In this paper, Annealed Demon (AD) [15] method is proposed for solving the EED problem in power system.
Simulated Annealing (SA) Algorithm
The basis of SA algorithm has built on the manner in which metals re-crystallise in the process of annealing. It begins at a high temperature where a metal is slowly cooled, so that the system is in thermal equilibrium at every stage. At high temperature the metal is in liquid phase. By gradually cooling of the metal, the system freezes into a minimum energy crystalline structure that is reaching a globally minimum value [16].
Suppose a state of the metal with energy Ei and subsequent energy state Ej. If ΔΕ=Ej-Ei<=0, then state j is accepted as current state, otherwise it is accepted with probability
|
|
(1) |
where T is the current temperature and KΒ is Boltzann’s constant.
The SA algorithm starts with an initial solution Si. A neighborhood, sj, of the solution is generated and the change in cost Δf(Si,Sj) is calculated. If a reduction in cost is found, the current solution is replaced by the neighboring solution otherwise the neighboring solution is accepted with a certain probability.
The probability of accepting a new solution is given [16]:
|
|
(2) |
where T is the control parameter that corresponds in the analogy with annealing process.
For the solution of an optimization problem with SA algorithm the following steps are required:
§ Step 1: Find, randomly, an initial solution, which is assigned as the current solution xi .
§ Step 2: Determine the initial value of the control parameter of temperature T(O) = Tinit
§ Step 3: Find a neighboring solution xj, being i.e. a heuristic strategy and calculate the new value of the objective function f(xj)
§
Step 4: if f(xj)<=f(xi), accept the trial
solution, otherwise if f(xj)>f(xi) calculate the
difference of the objective function Δf = f(xj)-f(xi) and accept the new
solution according to the probability ![]() otherwise
go to step 6
otherwise
go to step 6
§ Step 5: Set xi = xj and f(xi)=f(xj) and calculate the current simulated temperature with coefficient α (0<α<1) and decrease the simulated temperature gradually at every iteration, so that at (k+1) iteration: T(k+1) = aTk , where k is the iteration index.
§ Step 6: If the current simulated temperature is low, according to a cooling schedule, accept the current solution as being optimum, otherwise go to step 3.
Demon Algorithm
The Demon algorithm is an improved generalization of the SA algorithm [17]. The need of finding such an algorithm derived from the analysis of stochastic heuristic algorithms, where we must find the minimum number of evaluations of the objective function of a problem. This is a necessity in order for the system to move from a small number of conditions to another. The sum of these conditions derives from a distribution which defines the probability of finding a specific solution into that group.
The main purpose of this stochastic search algorithm is the change of the conditions group which is achieved through a Boltzmann distribution sequence with continued lower temperatures [18].
In general, the demon algorithm replaces the check of the acceptance probability with a variable named “Demon”. When the algorithm accepts a new solution of better cost it adds the cost difference to the demon variable. When the algorithm accepts a worse solution it subtracts the cost difference from the demon variable. While Demon has a value that can “afford” worse solutions it continues accepting them.
For the application of the demon algorithm we must consider the following
1. States of the system: they correspond to the acceptable solutions of a problem.
2. Energy : it corresponds to the cost of the objective function
3. Demon : it corresponds to a parameter that controls the acceptance probability of a solution
4. Cooling condition: Optimal solution of the algorithm.
The steps of the Demon Algorithm are [16]:
Step 1. Choose an initial state Si
Step 2. Choose an initial demon energy D=D > 0
Step 3. Repeat
a) choose a new state Sj
b) let ΔΕ=E(Sj)-E(Si)
c) if ΔΕ<=D accept new state and update Demon, i.e. Sj=Si, D=D-ΔΕ
d) else reject new state
Step 4. Until Stop_Condition
Annealed Demon (AD) Algorithm
The best form of the demon algorithm is the annealed demon. Annealed demon combines the benefits of the classic demon algorithm along with those from simulated annealing algorithm. In particular it exploits the calculation speed of the demon algorithm and it also gives solutions of high quality. In order to do that the Annealed demon algorithm reduces the demon variable in a manner similar to the reduction of the temperature in the simulation annealing. The steps of the Annealed demon algorithm are :
1. Choose initial state Si
2. Choose an initial demon energy D=Do>0
3. repeat
(i) choose a new state Sj
(ii) let ΔΕ = E(Sj)-E(Si)
(iii) if ΔΕ<D accept new state and update demon, i.e. Sj=Si , D=D-ΔΕ
(iv) else reject new state
(v) if equilibrium reached, reduce Demon according to schedule, i.e. D=a*D
4. until stop condition
Problem Formulation
The EED problem is to minimize simultaneously two conflicting objectives i.e. fuel cost and emission, while satisfying several equality and inequality constraints. The problem is formulated as follows.
Objective Functions
Minimize of Fuel Costs
The problem of an economic load dispatch (ELD) is to find the optimal combination of power generation which minimizes the fuel cost, under some constraints [19]. The ELD problem can be mathematically formulated as the following optimization problem:
Minimize
|
|
(3) |
where: Fc = the total fuel cost ($/hr); αi,bi,ci = the fuel cost coefficients of generator ith; PGi = the power generated by generator ith (MW); n = the number of generators;
The emission dispatch problem including the SO2 and NOx emission objectives, can be modeled using second order polynomial functions [20]:
Minimize
|
|
(4) |
Minimize
|
|
(5) |
Units of ESO2 and ENOx are ton/h.
Problem Constraints
Power Balance Constraints
The total power generation must cover the total demand, PD(MW) and the real power loss, PL(MW) in transmition lines. Hence
|
|
(6) |
The transmission losses are given by:
|
|
(7) |
where PL = Power loss, Bij = transmition losses coefficients, PGi=Power generated by ith generator, PGj = Power generated by jth generator.
Generation Capacity Constraints
The power output of each generator should lie between it’s minimum and maximum limits.
|
|
(8) |
where: PGimin = minimum power generated, and PGimax = maximum power generated.
Implementation of Annealed Demon (AD) Algorithm in Environmental/Economic Dispatch (EED) Problem
The steps of the algorithm (AD) in order to solve the EED problem are :
· Step 1. Initialization of the demon value and definition of the termination criterion (number of repetitions). Selection of an initial random solution state, which derives from the calculation of the total cost (objective function) in order to meet the criteria from restrictive conditions (6) and (8).
· Step 2. Find a neighboring solution through a random perturbation of the counter one in respect to the restrictive conditions (6) and (8)
· Step 3. Calculate the new total cost of the objective function (Fc)
· Step 4. If the new solution is better then we accept it and we add the Energy Difference (ΔΕ) to the demon variable. If the new solution is worse then we accept it and we subtract the energy difference (ΔΕ) to the demon variable. Worst Solutions are accepted only if the demon variable has enough big value to “pay” for the (ΔΕ) of the worst solution.
· Step 5. We decrease the demon variable by a factor α* EΔ = α*ΕΔ
· Step 6. If we don’t meet termination criteria then go to Step 2
Case Study
The annealed demon (AD) algorithm was applied to a 3 generator test system [19] whose data are given below. The system demand is 850 MW.
Table 1. Fuel Cost Coefficients
|
Unit i |
ai |
bi |
ci |
PGi min |
PGi max |
|
1 |
561.0 |
7.92 |
0.001562 |
150.0 |
600.0 |
|
2 |
310.0 |
7.85 |
0.00194 |
100.0 |
400.0 |
|
3 |
78.0 |
7.97 |
0.00482 |
50.0 |
200.0 |
|
αi,bi,ci = the fuel cost coefficients of generator ith; PGi min = minimum power of generator ith PGi max = maximum power of generator ith |
|||||
The transmition losses are calculated using a simplified loss expression:
PL = 0.00003PG12 + 0.00009PG22 + 0.00012PG32
SO2 and NOx emission coefficients are taken from [20] and are shown in tables 2 and 3 respectively
Table 2. SO2 Emission coefficients
|
Unit i |
ais |
bis |
cis |
|
1 |
1.6103e-6 |
0.00816466 |
0.5783298 |
|
2 |
2.1999e-6 |
0.00891174 |
0.3515338 |
|
3 |
5.4658e-6 |
0.00903782 |
0.0884504 |
|
aiS,biS,ciS = coefficients of SO2 emissions (see eq.4) |
|||
Table 3. NOx Emission coefficients
|
Unit i |
aiN |
biN |
ciN |
|
1 |
1.4721848e-7 |
-9.4868099e-5 |
0.04373254 |
|
2 |
3.0207577e-7 |
-9.7252878e-5 |
0.055821713 |
|
3 |
1.9338531e-6 |
-3.5373734e-4 |
0.027731524 |
|
aiN,biN,ciN = coefficients of NOx emissions (see eq.5) |
|||
Simulation of the (AD) Algorithm
In table 4 we present the results for the (AD) algorithm. In our simulations
the demon value is 100, temperature is 100, alpha factor is 0.9 and repetitions
we choose 1000. All the simulations made in a Core 2 Duo at 1.8 GHz with 2GB
RAM. The programming language we used is
Table 4. Minimum values of individual objectives
|
Number of execution |
Fuel Cost |
Emissions of SO2 |
Emissions of NOx |
|
1 |
8.344.593 |
8.990 |
0.096 |
|
2 |
8.362.288 |
8.968 |
0.097 |
|
3 |
8.387.265 |
8.966 |
0.1 |
|
4 |
8.357.183 |
9.020 |
0.098 |
|
5 |
8.359.827 |
9.000 |
0.098 |
|
6 |
8.376.034 |
8.966 |
0.096 |
|
7 |
8.377.415 |
9.019 |
0.114 |
|
8 |
8.344.593 |
8.971 |
0.096 |
|
9 |
8.388.149 |
9.014 |
0.098 |
|
10 |
8.344.725 |
8.968 |
0.096 |
Final Solution - Convergence Solution - Compromise Solution
From the above results we have now 3 optimum solutions for the 3 objective functions which define
· Best Fuel Cost
· Best SO2 Emissions
· Best NOx Emissions
There are many theories for finding the best compromise solutions like the fuzzy logic theory. One of them is the simple average. In order to apply the simple average to our results we must take the best results we have come up with. Then we must calculate the average of the two power generators. The third power generator value will derive after we solve a second degree equation. Then we will simply replace the PG1, PG2 and PG3 to our initial equations and we will have the final compromise solution.
Table 5. Best Solutions so far
|
|
Best Fuel Cost |
Best SO2 Emission |
Best NOx emission |
|
PG1 |
435.237 |
552.187 |
473.696 |
|
PG2 |
300.088 |
219.466 |
285.204 |
|
PG3 |
130.507 |
92.864 |
106.514 |
|
Losses |
15.832 |
14.517 |
15.414 |
|
Fuel Cost |
8.344.593 |
8.396.533 |
8.351.418 |
|
SO2 Em. |
9.022 |
8.966 |
8.992 |
|
NOx Em. |
0.099 |
0.097 |
0.096 |
Initially we find the average of PG1 and PG2.
PG1 = (435.237 + 552.187 + 473.696) / 3 = 487.040
PG2 = (300.088 + 219.466 + 285.204) / 3 = 268.253
In order to find PG3 we must solve the following equation: ΣPi – PD – PL = 0 which will end up to a second degree polynomial with PG3 as the unknown value. We solve and we come up with PG3 = 109.745
Since we have the PG1, PG2, PG3 values we put them to the initial equations. The following table shows the best compromise solution.
Table 6. Best compromise solution
|
PG1 |
487.040 |
|
PG2 |
268.253 |
|
PG3 |
109.745 |
|
Losses |
15.038 |
|
Fuel Cost |
8.354.982 |
|
SO2 Em. |
8.983 |
|
NOx Em. |
0.096 |
Conclusions
An annealed Demon (AD) algorithm has been used for solving the environmental/economic dispatch problem. In general an optimization problem is considered where simulation results on a 3-generator test system considering fuel cost, SO2 emission and NOx emission have been presented. The system demand is 850 MW in all simulations. We considered 3 different objective functions and through them we founded best fuel cost, best SO2 emission, and best NOx emission
For the final compromise solution we used the simple average method.
References
1. Lee K. Y., Yome A. S., Park J. H., Adoptive Hopfied neural networks for economic load dispatch, IEE Transactions on Power Systems, 1998, 13(2), p. 519-526.
2. Petrovic R., Kralj B., Economic and environmental power dispatch, European Journal of Operation Research, 1993, 61(1), p. 2-11.
3. Talaq J. H., EI-Hawary F., EI-Hawary M. E., A Summary of environmental/economic dispatch algorithms, IEEE Transactions on Power Systems, 1994, 9(3), p. 1508-1516.
4. Wang L.F., Singh C., Environmental / Economic Dispatch using a fuzzified multi-objective particle swarm optimization algorithm, Electric Power System Research, 2007, 77(12), p. 1654-1664.
5. Papiya D., Sinha A.K., Environmental economic dispatch constrained by voltage stability using PSO, In: Proceedings of IEEE International Conference on Industrial Technology, 2006, p. 1879-1884.
6. Jayabarathi T., Sadasivarm G., Ramachandran V., Evolutionary programming based multi-area economic dispatch with tie line constraints, Electric Machines and Power Systems, 2000, 28, p. 1165-1176.
7. King R. T. F. A., Rughooputy H. C. S., Deb K., Stochastic evolutionary multi-objective environmental/economic dispatch, In: Proceedings of IEEE congress on Evolutionary computation, 2006, p. 946-953.
8. Abido M. A., Environmental /Economic Power Dispatch using multiobjective evolutionary algorithms, IEEE Transactions on Power Systems, 2003, 18(4), p. 1529-1537.
9. Huang C. M., Yang H. T., Huang C. L., Bi-objective power dispatch using fuzzy satisfaction-maximizing decision approach, IEEE Transaction on Power Systems, 1997, 12, p. 1715-1721.
10.
Abido M. A., A new multiobjective evolutionary algorithm for
environmental/economic power dispatch, IEEE Summer Meeting,
11. Chen S.-L., Tsay M.-T., Gow H.-J., Scheduling of cogeneration plants considering electricity wheeling using enhanced immune algorithm, International Journal of Electrical Power and Energy Systems, 2005, 27(1), p. 31-38.
12.
Song Y. H., Wang G. S., Wang P. Y., Johns A. T., Environmental /
Economic dispatch using fuzzy logic controlled genetic algorithms,
13. Chaturvedi K. T., Pandit M., Srivastava L., Modified neo-fuzzy neuron based approach for economic and environmental optimal power dispatch, Applied Soft Computing, 2008, 8(4), p. 1428-1438.
14. Das D. B., Patvardhav C., New multiobjective stochastic search technique for economic load dispatch, IEE Proceedings-Generation, Transmission and Distribution, 1998, 145(6), p. 747-752.
15.
Wood I.,
16. Kirkpatcick S., Gelatt C. D., Vecchi M. P., Optimization by Simulated Annealing, Science, 1983, 220, p. 671-680.
17. Zimmermann T., Salamon P., The demon algorithm, Futern. J. Computer Math., 1992, 42, p. 21-31.
18. Salamon P., Hoffman K. H., Harland J., Nulton J.D., An information theoretic bound on the performance of simulated annealing algorithms, SDSU IRC report, 1988, 88-1.
19. Wood A. J., Wollenberg B. F., Power generation, operation and control, John Wiley and sons; IMC, 1984.
20. Foa-Sepulveda C. A., Salazar-Nova E. R., Gracia-Caroca E., Knight U. G., Coonic A., Environmental Economic Dispatch via Hopfield Neural Network and Taboo Search, UPEC’96 Universities power engineering conference, Crete, Greece, 18-20 September 1996, p. 1001-1004.