A Hybrid Tabu Search and Algorithm Genetic for Solving the Economic Dispatch Problem
Bakhta NAAMA1 , Hamid BOUZEBOUDJA1, Mohamed LAHDEB2, Youcef RAMDANI3
1 Electrotechnical Department, Faculty of Electrical
Engineering, USTO,
2 Electrotechnical Department,
Faculty of Electrical Engineering, University
3Electrotechnical Department, Faculty of Electrical Engineering, University Djillali Liabes, Algeria.
E-mail(s): naamasabah@yahoo.fr; hbouzeboudja@yahoo.fr; mlahdeb@yahoo.fr; remdaniy@yahoo.fr
Tel/Fax: +21341425509
Abstract
The application of optimization techniques to power system planning and operation problems has been an area of active research in the recent past. Genetic Algorithm (GA), Tabu Search (TS) are widely used to combinatorial optimization in recent years. Combining the advantages of individual algorithms, a hybrid TS/GA algorithm to solve the economic dispatch problem is proposed in this paper, using the method of penalty to transform the problem ED with constraints in a simple problem without constraints. An IEEE 57-bus power system has been used to test the proposed algorithm. Comparing the results of the proposed algorithm with GA, TS and proposed TS/GA hybrid method has the strongest capability of finding global optimal solution within reasonable computing time. We then give a comparison between two algorithms hybrids (Tabu Search / Genetic Algorithm) TS/GA and (Tabu Search/ quasi-Newton method) TS/QN.
Keywords
Economic Dispatch; Optimization; Metaheuristic; Genetic Algorithm (GA); Tabu Search (TS); Quasi-Newton Method; Hybrid Approach.
Introduction
The economic dispatch (ED) is an optimization problem to find the most economical schedule of the generating units while satisfying load demand and operational constraints. This problem has been tackled by many researchers in the past. The literature of the ED problem and its solution methods are surveyed in [1, 2].
This paper reports about the hybrid algorithm that determines the optimum distribution network configuration. The hybrid algorithm that was integrated by Genetic Algorithm (GA) and Tabu Search (TS) was studied in order to bring out each strong point and compensate for each demerit. We developed GA and TS hybrid Algorithm, and succeeded in obtaining optimum solution with high speed and high precision.
Economic Dispatch
Economic dispatch is the important component of power system optimization [3]. It is defined as the minimization of the combination of the power generation, which minimizes the total cost while satisfying the power balance relation. The problem of economic dispatch can be formulated as minimization of the cost function subjected to the equality and inequality constraints.
Minimize the cost function:
|
|
(1) |
where F (Pi) is the total cost, ![]() the generator
cost coefficients and Pi is the power generation.
the generator
cost coefficients and Pi is the power generation.
Subjected to the constraints:
¸ Power balance (equality constraints)
|
|
(2) |
where PD is the power demand and PL is the power loss.
¸ Threshold limits (inequality constraints)
|
|
(3) |
where ![]() and
and
![]() are
the minimum and maximum power generation limits.
are
the minimum and maximum power generation limits.
The equality constraint from equation (2) is formulated as a constraint violation relation as:
|
|
(4) |
The total objective function is the sum of the cost function and the constraint violation. We applying a penalty function we transform a constrained non-linear ED problem into a constrained problem:
|
|
(5) |
where the value of the penalty coefficient rk is checked at each iteration.
The Genetic Algorithm
Genetic algorithm, which imitates the selection and biological
evolutionary process, is a well-known structured random search method [4]. An
important aspect of GA as stressed by
GA has the following features that distinguish itself from other heuristics: (a) a large number of feasible points in the solution space are searched and evaluated simultaneously, (b) the strings of characters which represent the parameter set are dealt with directly, and (c) the probabilistic theory, not a deterministic selection, is used to direct their search. Therefore, GA can decrease the possibility of being trapped into a local minimum and often produces high quality solutions in a shorter period of time. Despite of its effectiveness, several issues yet need to be explored in order to get good solutions:
o The representation of chromosome.
o The generation of initial populations.
o The selection of fitness function.
o The selection and design of heuristic genetic operators: reproduction, crossover and mutation [11].
The determination of system parameters: population size, # of generations, crossover probability, mutation probability.
Selection is the process by which strings with better fitness values receive correspondingly better copies in the new generation. That is the more fitness string solutions should have more chances to be copied to the next generation population. The task of crossover is the creation of new individuals (children), out of two individuals (parents) of the current population. Mutation is a background operator, which produces spontaneous random changes in various chromosomes. A simple way to achieve mutation would be to alter one or more genes. In genetic algorithms, mutation serves the crucial role of either replacing the genes lost from the population during the selection process so that they can be tried in a new context or providing the genes that were not present in the initial population [12].
Tabu Search
Tabu search is a metaheuristic that is used to manage a local method to search the solution space without entrapping into a local optimum by means of some strategies. The term “Tabu Search” first appeared in literatures in Glover’s paper (1986) [13]. Hansen (1986) [14] brought up a similar idea and called it “the steepest ascent/mildest descent heuristic”.
Tabu search is an iterative search method. It uses a local search algorithm at each iteration to search for the best solution in some subset of the neighborhood, which came from the best solution obtained at the last iteration. At each iteration, the local search algorithm looks for the best improving solution. If all solutions are not improving the objective function value, then it looks for the least deterioration solution. Tabu search keeps a list, which is called tabu list, of the moves it used to obtain the best solutions during each iteration and to restrict the local search algorithm in reusing those moves. A memory is used to keep track of this tabu list. Usually the tabu list has a pre-specified length. Therefore, this list varies from iterations to iterations.
There are mainly three strategies employed in tabu search: the forbidding strategy, the freeing strategy and the short-term strategy. The foebidding strategy what enters the tabu list. The freeing strategy decides what exits the tabu list and when the exit will occur. The short-term strategy manages the interplay between the forbidding strategy and freeing strategy to generate and select trial solutions [15].
Hybrid TS /GA Algorithm
Hybridization is a trend in many works on metaheuristics past ten years. It takes advantage of the benefits accrued from different metaheuristics, so much so that the basic metaheuristics are nothing more than canvas, starting points to begin to solve an optimization problem [18].
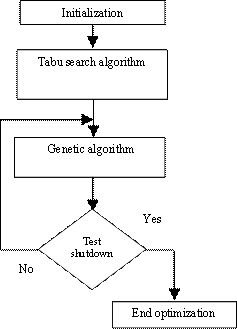
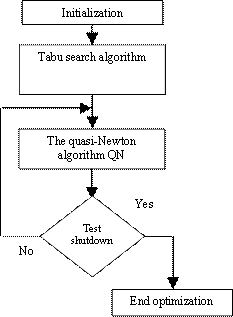
In the figures below, we propose an optimization method based on a hybrid approach. The basic idea is to make a combination between the basic metaheuristics TS/AG on one hand and the other to a combination of analytical methods and metaheuristics as TS/QN.
|
|
|
|
Figure 1. TS/GA hybrid algorithm |
Figure 2. TS/QN hybrid algorithm |
Numerical Results
The IEEE 57-bus power system has been tested using MATLAB-R12 on PC-Pentium 2 GHz. The IEEE 57-bus power system [16] consists of 7 generator buses, 42 load buses, and 78 branches. The fuel cost in ($/hr) equations for the generator are:
F1 (PG1) = 0.0776 PG12 + 20 PG1 + 0.0 F2 (PG2) = 0.0100 PG22 + 40 PG2 + 0.0 F3 (PG3) = 0.2500 PG32 + 20 PG3 + 0.0 F6 (PG6) = 0.0100 PG62 + 40 PG6 + 0.0 F8 (PG8) = 0.0222 PG82 + 20 PG8 + 0.0 F9 (PG9) = 0.0100 PG92 + 40 PG9 + 0.0 F12 (PG12) = 0.0323 PG122 + 20 PG12 + 0.0
And the constraints are: (the unit operating ranges in MW):
00 ≤ PG1 ≤ 575.88; 00 ≤ PG2 ≤ 100; 00 ≤ PG3 ≤ 140; 00 ≤ PG6 ≤ 100; 00 ≤ PG8 ≤ 550; 00 ≤ PG9 ≤ 100; 00 ≤ PG12 ≤ 410
The total load was 1250.8 MW.
Transmission losses PL are computed using B coefficients.
Ø Parameters values for GA
The parameters values for GA have a number of population size, crossover and mutation probability, chromosomes length and number of generations [17]:
· Population size: 30;
· Crossover probability: 0.75;
· Mutation probability :0.006
· Chromosomes length: 12;
· Number of generations: 300.
Ø Parameters values of TS
The parameters values of TS have a tabu list length, Number of neighborhood, Number of diversification and number of generations:
· Tabu list length:10;
· Number of neighborhood:45;
· Number of diversification :1;
· Number of generations: 200.
The minimum cost and active power are presented in table 1.
Table 1. Result of GA, TS and hybrid approach
|
|
GA |
TS |
TS/GA |
TS/QN |
|
PG1opt (MW) |
146.2465 |
253.3952 |
148.2892 |
140.3763 |
|
PG2opt (MW) |
74.3569 |
97.4596 |
97.1834 |
89.0284 |
|
PG3opt (MW) |
50.7484 |
94.1011 |
42.5183 |
43.5614 |
|
PG6opt (MW) |
75.0733 |
40.5436 |
74.7205 |
89.0284 |
|
PG8opt (MW) |
508.5059 |
528.1956 |
509.5681 |
490.0618 |
|
PG9opt (MW) |
75.3609 |
94.2480 |
75.9688 |
89.0283 |
|
PG12opt (MW) |
348.3446 |
170.6614 |
330.4420 |
337.5974 |
|
Cost ($/hr) |
42201 |
44760 |
42190 |
42170 |
|
Time (s) |
1.76 |
1.18 |
1.29 |
1.12 |
Results
The hybridization TS/GA and TS/QN gives better fuel cost with a reasonable amount of time compared to GA and TS.
The results found by the analytical methods QN remains always the best because these methods converge to the optimum quickly that the inverse methods metaheuristics and for this reason the propose hybridization method to combine between advantages analytical methods and metaheuristic methods.
The proposed technique improves the quality of the solution and reduces the computation time.
Conclusions
In this paper we applied the method of combinatorial optimization metaheuristics as a means of minimizing the cost of producing a network standard IEEE-57, where we have used genetic algorithms, tabu search. We also presented a hybrid between the methods mentioned above TS /GA. A comparison was made between TS /GA and TS / QN.
The genetic algorithm performed better cost point of view, but a higher computation time compared to the tabu search. The hybridization between the based metaheuristics such as GA and TS gives better fuel cost with a reasonable amount of time compared to the second hybridization (TS /Q N).
References
1. Happ H. H., Optimal power dispatch - A comprehensive survey, IEEE Trans. Power App. Syst., 1977, PAS-96, p. 841-854.
2. Chowdhury B. H., Rahman S., A review of recent advances in economic dispatch, IEEE Trans. on Power Systems, 1990, 5(4), p. 1248-1259.
3. Swarup K. S., Economic Dispatch Solution using Hopfield Neural Network, Journal- Institution of Engineers India Part El Electrical Engineering Division, 2004, 84, p. 77-82.
4. Chu C.-H., Tsai C.-C., A Heuristic Genetic Algorithm for Grouping Manufacturing Cells, Proceedings of the 2001 Congress on Evolutionary Computation, 2001, 1, p.310-317.
5.
6. Gen M., Cheng R., Genetic Algorithms and engineering design, MA: Wiley Interscience Publication, 1997.
7.
Goldberg D. E., Genetic Algorithms in Search Optimization, and
Machine Learning, Addison-Wesley,
8. Hedberg S., Emerging genetic algorithms, AI EXPERT, 1994, 9, p. 25-37.
9.
Reeves C. R., A Genetic Algorithm for flow shop scheduling,Working
Paper, Department of Statistics and Operations Research,
10. Tam K. Y., Genetic Algorithms, function optimization, and facility layout design, European J. of Operational Res., 1992, 63, p. 322-346.
11.
Abdullah W. N. W, Saibon H., Zain A. A. M., Lo K. L., Genetic Algorithm for Optimal
Reactive Power Dispatch,
12. Goldberg D. E., Optimisation et apprentissage automatique, Edition Addison Wesley France 1991.
13. Glover F., Future Paths for Integer Programming and Links to Artificial Intelligence, Computers and Operations Research, 1986, 13, p. 533-549.
14.
Hansen P., The Steepest Ascent
Mildest Descent Heuristic for Combinatorial Programming, Congress on
Numerical Methods in Combinatorial Optimization,
15. Hanafi S., On the Convergence of Tabu Search, Journal of Heuristics, 2001, 7, p. 47-58.
16. Zimmerman R., Gan D., MATPOWER: A MATLAB Power System Simulation Package, 1997.
17. Naama B., Bouzeboudja H., Ramdani Y., Chaker A., Hybrid Approach to the Economic Dispatch Problem Using a Genetic and a Quasi-Newton Algorithm, Acta Electrotechnica et Informatica, 2008, 8(3), p. 31-35.
18. Bouzeboudja H., Chaker A., Allali A., Naama B., Economic Dispatch Solution Using a Real-Coded Genetic Algorithm, Acta Electrotechnica et Informatica, 2005, 5(4), p. 1-5.