Different versions of Harmony Search Algorithm to Solve Dynamic Economic-Environmental Dispatch
Abderrahim BELMADANI1, Lahouaria BENASLA2* and Mustapha RAHLI2
1Department of Computer Science
U.S.T.O, B.P 1505,
2Department of Electrical
Engineering,U.S.T.O, B.P 1505,
E-mail(s): jbenasla@yahoo.fr; belmadan@univ-usto.dz; rahlim@yahoo.fr
Abstract
This paper presents an application of different versions of Harmony Search algorithm (Harmony Search Algorithm (HSA), Improved Harmony Search Algorithm (IHSA), Global Harmony Search Algorithm (GHSA) and Fast Harmony Search algorithm (FHSA)) to solve the Dynamic Economic-Environmental Dispatch (DEED) problem under some equality and inequality constraints. The equality constraints reflect a real power balance, and the inequality constraint reflects the limits of real generation. The voltage levels and security are assumed to be constant. Dynamic Economic-Environmental Dispatch problem is obtained by considering both the economy and emission objectives. This bi-objective problem is converted into a single objective function using a price penalty factor.
In this paper different versions of HSA are tested on six generators system and its results are compared with the previously published solutions. The results are quite encouraging and useful in the economic emission environment.
Keywords
Dynamic Economic-Environmental Dispatch (DEED); Pollution Emission; Fuel cost; Harmony Search Algorithm (HSA); Improved Harmony Search Algorithm (IHS); Global Harmony Search Algorithm (GHSA); Fast Harmony Search Algorithm (FHSA).
Introduction
Evolutionary algorithms are general-purpose stochastic search methods simulating natural selection and biological evolution. They differ from other optimization methods in the fact maintaining a population of potential solutions to a problem, and not just one solution. Generally, these algorithms work as follows: a population of individuals is randomly initialized where each individual represents a potential solution to the problem. The quality of each solution is evaluated using a fitness function. A selection process is applied during each iteration in order to form a new solution population. This procedure is repeated until convergence is reached. The best solution found is expected to be a near-optimum solution.
HSA that was proposed by Greem and al. [2] is an evolutionary algorithm imitating the improvisation process of musicians. This process is constituted of three steps, in the original HSA, with a fourth step added in the improved version [3]. In order to improve the fine–tuning characteristic of HSA, Mahdavi and al. [4] developed an Improved Harmony Search Algorithm (IHSA) that differs from original HSA in the fact that some parameters (pitch adjusting rate “PAR” and bandwidth “bw”) are adjusted during the improvisation process. Omran and al [5] proposed another version of HSA named Global-best Harmony Search Algorithm (GHSA), which borrows concepts from swarm intelligence to enhance the performance of HSA. GHSA is an IHSA version with the pitch-adjustment modified such that the new harmony can mimic the best harmony in the Harmony Memory (HM). Our version of HSA (FHSA), is inspired by the concept of reactive search [6] where parameter tuning, which is usually performed offline by the researcher, becomes an integral part of the search algorithm, ensuring flexibility without human intervention. The "learning" component is implemented as a reactive feedback scheme that uses the past history of the search to increase its efficiency and efficacy.
Economic dispatch is one of the most important optimization problems in power system operation and forms the basis of many application programs. The main objective of economic load dispatch of electric power generation is to schedule the committed generating unit outputs so as to meet the load demand at minimum operating cost while satisfying all unit and system constraints. One of those constraints which are always taken into account is the environmental constraint. That is minimization of pollution emission (NOx, CO2, SO2, small quantities of toxic metals, etc) in case of power plants. However, the rise of interests in environment problem in the recent years, it become necessary for power utilities to count this constraint as one of the main objectives, which should be solved together with the cost problem [7, 8]. Thus, we are facing with a bi-objective optimization problem to deal with. This problem is converted into mono-objective optimisation problem by introducing price penalty factor.
In this paper, different versions of HSA are applied to solve DEED problem. A six generators system is considered to investigate the effectiveness of the proposed versions.
Problem Formulation
Economic Dispatch
Economic dispatch is the important component of power system optimization. It is defined as the minimization of the combination of the power generation, which minimizes the total cost while satisfying the power balance relation. The problem of economic dispatch can be formulated as minimization of the cost function subjected to the equality and inequality constraints [9].
In power stations, every generator has its input/output curve. It has the fuel input as a function of the power output. But if the ordinates are multiplied by the cost of $/Btu, the result gives the fuel cost per hour as a function of power output [10].
In the practical cases, the fuel cost of generator i may be represented as a polynomial function of real power generation:
![]() (1)
(1)
where ![]() is the total
fuel cost of the system at time t,
is the total
fuel cost of the system at time t, ![]() is real power output
at time t,
is real power output
at time t, ![]() is the number of generators including
the slack bus,
is the number of generators including
the slack bus,![]() ,
, ![]() and
and ![]() are
the cost coefficients of the ith unit.
are
the cost coefficients of the ith unit.
The total cost of active power generation may be expressed by:
![]() (2)
(2)
The Economic Dispatch Problem can be mathematically represented as:
Minimize ![]() (3)
(3)
Emission Dispatch
The emission function can be expressed as the sum of all types of emission considered, such as NOx, SO2, CO2, particles and thermal emissions, ect, with suitable pricing of weighting on each pollutant emitted [11].
In the present study, only emission of NOx is taken into account. The emissions function of the unit i can be expressed as polynomial function of real power generation of the unit. Therefore, the objective function is:
Minimize NOx emission
![]() (4)
(4)
Where ![]() is
NOx emission at time t and
is
NOx emission at time t and ![]() ,
, ![]() and
and ![]() are
the emission coefficients of the i-th unit
are
the emission coefficients of the i-th unit
Constraints
Equality Constraints
The total power
generation must cover the total demand ![]() and the real
power losses of the system
and the real
power losses of the system![]() .
Hence,
.
Hence,
![]() (5)
(5)
The real power losses
are a function of real power injection![]() and reactive power
and reactive power ![]() and
voltage nodes. Their expression is given by [12]:
and
voltage nodes. Their expression is given by [12]:
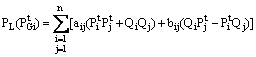
where![]() ,
, ![]() ,
, ![]() and
and ![]() ,
, ![]() is the total bus number,
is the total bus number, ![]() is the
active power demand at bus i,
is the
active power demand at bus i, ![]() is the reactive demand at bus i,
is the reactive demand at bus i, ![]() are
the real components of bus impedance matrix.
are
the real components of bus impedance matrix.
The voltages nodes ![]() (in
module
(in
module ![]() and phase
and phase![]() ) and the
reactive power injection are assumed constant. In this case, the power
transmission losses can be expressed in terms of active power generations by
assuming that the demand for power remains constant during dispatch period.
This expression is given by:
) and the
reactive power injection are assumed constant. In this case, the power
transmission losses can be expressed in terms of active power generations by
assuming that the demand for power remains constant during dispatch period.
This expression is given by:
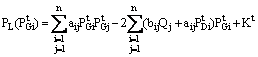
where 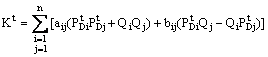
Inequality Constraints
Generation power should
be within the minimum output ![]() and the maximum output
and the maximum output![]() .
.
![]() (6)
(6)
Combined Economic and Emission Dispatch
Aggregating equations (1) to (6), the power dispatch problem is expressed as a bi-objective optimization problem as follows:
![]() (7)
(7)
The bi-objective combined economic
emission dispatch problem is converted into single optimization problem by
introducing price penalty factor ![]() as follows:
as follows:
![]() (8)
(8)
Subject to the power constraints given by (5) and (6).
The price penalty factor ![]() is the
ratio between the maximum fuel cost and maximum emission of corresponding
generator [13, 14]
is the
ratio between the maximum fuel cost and maximum emission of corresponding
generator [13, 14]
![]() (9)
(9)
The steps to determine the price penalty factor for a particular load demand are:
1. Find the ratio between maximum fuel cost and maximum emission of each generator.
2. Arrange ![]() in
ascending order.
in
ascending order.
3. Add the maximum
capacity of each unit![]() one at a time, starting from the
smallest
one at a time, starting from the
smallest ![]() until
until![]() .
.
4. In this stage, ![]() associated
with the last unit in the process is the price penalty factor of the given
load.
associated
with the last unit in the process is the price penalty factor of the given
load.
Once the value of ![]() is
known, then equation (8) can be rewritten in terms of known coefficients and
the unknown output of the generators.
is
known, then equation (8) can be rewritten in terms of known coefficients and
the unknown output of the generators.
![]() (10)
(10)
where ![]() ,
, ![]() and
and![]() ,
,
The Harmony Search Algorithms
Harmony Search Algorithm
The Harmony Search Algorithm (HSA) is inspired from the musical process of searching for a perfect state of harmony. All Harmony Search versions consider the optimization problem defined as:
![]()
Subject to: ![]()
The optimization process is directed by four parameters [2, 15]:
1. Harmony Memory Size (HMS) is the number of solution vectors stored in HM.
2. Harmony Memory Considering Rate (HMCR) is the probability of choosing one value from HM and (1-HMCR) is the probability of randomly choosing one new feasible value.
3. Pitch Adjusting Rate (PAR) is the probability of choosing a neighbouring value of that chosen from HM.
4. Distance bandwidth (bw) defines the neighbourhood of a value as [xj ± bw·U(0,1)]. U (0,1) is a uniform distribution between 0 and 1.
Another intuitively important parameter is the Number of Iterations (NI) which is the stop criterion of the three previous versions of HSA.
HSA works as follows:
Step 1: Initialize the problem and HSA parameters.
Step 2: Initialize HM by randomly generated (improvised) harmonies.
Step 3: Improvise a new harmony as follows:
for j=1 to p do
if ![]() then
then![]()
else (*Memory consideration*)
begin
![]()
if ![]() then
(*pitch adjustment*)
then
(*pitch adjustment*)
begin ![]()
endif
endif
done
Step 4: If the New Harmony (NH) is better than the Worst Harmony (WH) in HM then replace WH by NH.
Step 5: Reiter Steps 3 and 4 until satisfaction of the stop criterion.
Improved Harmony Search Algorithm
The IHSA dynamically updates PAR and bw in improvisation step (Step 3).
These two parameters change dynamically with generation number as follows: ![]()
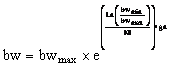
where: ![]() :
minimum pitch adjusting rate;
:
minimum pitch adjusting rate; ![]() : maximum pitch adjusting rate;
: maximum pitch adjusting rate; ![]() :
number of iterations;
:
number of iterations; ![]() : generation number;
: generation number; ![]() :
minimum bandwidth;
:
minimum bandwidth; ![]() : maximum bandwidth.
: maximum bandwidth.
Global Harmony Search Algorithm
The GHSA modifies the pitch adjustment step of the IHSA as follows:
if U(0,1) ≤ PAR then (*pitch adjustment*)
begin ![]()
endif
where best is the index of the best harmony in the HM and k ≈ U(1,p). This pitch adjustment is inspired by the concept of swarm intelligence in Particle Swarm Optimization. The position of a particle is influenced by the best position visited by itself and the best particle in the swarm.
Fast Harmony Search Algorithm
FHSA [16, 17] introduces a prohibition step between step 4 and step 5. It consists in defining a permanent prohibition of the search space (bounds adjustment) to prevent the system from going back on its track and is performed as follows:
for j=1 to p do
if ![]() then
then ![]()
else if ![]() then
then
![]()
else ![]()
endif
done
The stop criterion becomes:
if ![]()
![]() then
STOP endif
then
STOP endif
where![]() is a real
number “small enough” and
is a real
number “small enough” and![]() is the precision term.
is the precision term.
Application
All applications have
been performed using ERELEC2 (Etude des Réseaux ELECtriques V2) software. The
software has been developed by LORE (Laboratoire d’Optimisation des Réseaux
Electriques) laboratory at the
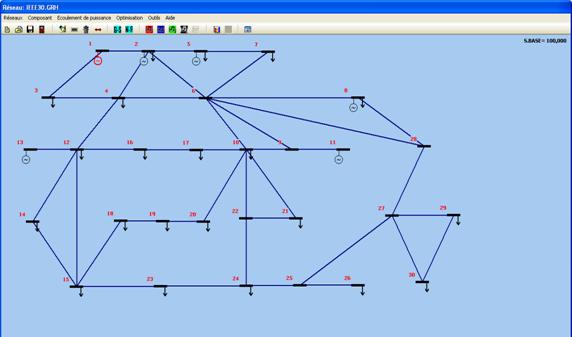
Figure 1. IEEE 30-bus system in ERELEC2
The generator fuel cost, and NOx emissions function are given in Tables 1 and 2.
Table1. The generator fuel cost
|
Bus |
Minimum output
|
Maximum output
|
Fuel cost
|
||
|
Cost coefficient
|
Cost coefficient
|
Cost coefficient
|
|||
|
1 |
50 |
200 |
0.00375 |
2.0 |
0 |
|
2 |
20 |
80 |
0.00175 |
1.5 |
0 |
|
5 |
15 |
50 |
0.06250 |
1.8 |
0 |
|
8 |
10 |
40 |
0.00834 |
2.0 |
0 |
|
11 |
10 |
30 |
0.02500 |
1.5 |
0 |
|
13 |
12 |
40 |
0.02500 |
1.8 |
0 |
Table 2. The NOx emissions function
|
BUS |
Emission function
|
||
|
Emission coefficient
|
Emission coefficient
|
Emission coefficient
|
|
|
1 |
6.490 e-6 |
5.554 e-4 |
4.091e-2 |
|
2 |
5.638 e-6 |
6.047 e-4 |
2.543 e-2 |
|
5 |
4.586 e-6 |
5.094 e-4 |
4.258 e-2 |
|
8 |
3.380 e-6 |
3.550 e-4 |
5.326 e-2 |
|
11 |
4.586 e-6 |
5.094 e-4 |
4.258 e-2 |
|
13 |
5.151 e-6 |
5.555 e-4 |
6.131 e-2 |
The daily load demands of IEEE 30-bus system are shown in Figure 2.
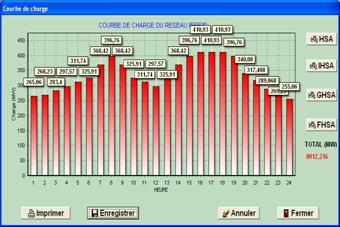
Figure 2. Daily load curve of IEEE 30-bus system in ERELEC2
The total system load of IEEE 30-bus system is 283.4 MW. The corresponding coefficients losses are:
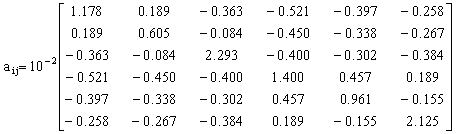 ,
,
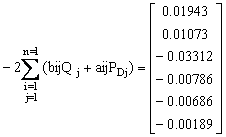 and K = 0.00364.
and K = 0.00364.
The NOx price penalty factors are given in Table 3
Table 3. The NOx price penalty factors.
|
Dispatch periods |
Price penalty factor
|
Dispatch periods |
Price penalty factor
|
|
1 |
3380.4055 |
13 |
7217.8478 |
|
2 |
3380.4055 |
14 |
19182.1697 |
|
3 |
3579.9067 |
15 |
19182.1697 |
|
4 |
3579.9067 |
16 |
19182.1697 |
|
5 |
7217.8478 |
17 |
19182.1697 |
|
6 |
7217.8478 |
18 |
19182.1697 |
|
7 |
19182.1697 |
19 |
19182.1697 |
|
8 |
19182.1697 |
20 |
7217.8478 |
|
9 |
19182.1697 |
21 |
7217.8478 |
|
10 |
7217.8478 |
22 |
3579.9067 |
|
11 |
7217.8478 |
23 |
3380.4055 |
|
12 |
3579.9067 |
24 |
3380.4055 |
The parameters of the different versions of HSA are resumed in Table 4.
Table 4. The parameters of the algorithms.
|
Version |
Parameters |
|
Harmony Search Algorithm (HSA) |
|
|
Improved Harmony Search Algorithm (IHSA) |
|
|
Global Harmony Search Algorithm (GHSA) |
|
|
Fast Harmony Search Algorithm (FHSA) |
|
HSA, IHSA and GHSA were allowed to run for 50,000 iterations with these common parameters: HMCR = 0.9; HMS = 14.
Figure 3 shows the result of the DED problem (cost optimization). The FHSA outperforms the other versions with a daily cost of 24 099.184 $/day, which corresponds to a gain of at least 50.71 $/day and more than 18 000 $/year.
The results of the four optimization methods are compared, for the third hour (load=283.4 MW) with those obtained in [1]. Table 5 shows that all Harmony Search based algorithms outperforms the Genetic Algorithm in the case of ED and FHSA is gives the best solution of all.
Table 5. DED results comparison
|
Algorithm |
Generation cost ($/hr) |
Power losses (MW) |
|
Genetic Algorithm [1] |
803.1060 |
9.9308 |
|
HSA |
798.884 |
9.021 |
|
IHSA |
800.584 |
9.085 |
|
GHSA |
799.571 |
8.958 |
|
FHSA |
788.887 |
8.608 |
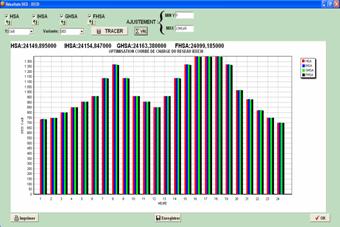
Figure 3. DED daily cost for IEEE 30-bus system in ERELEC2
The DEED results for the different versions of HSA are depicted in figures 4 to 6.
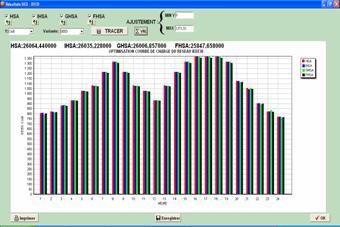
Figure 4. DEED daily Generation cost for IEEE 30-bus in ERELEC2
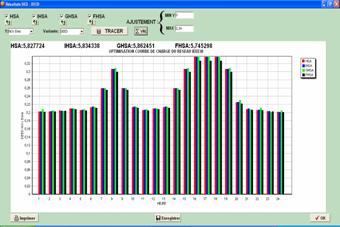
Figure 5. DEED daily NOx Emissions in ERELEC2
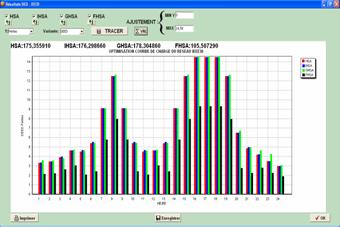
Figure 6. DEED daily Power losses in ERELEC2.
These graphs clearly indicate that total fuel cost, transmission losses and NOx emissions increase by increasing the power demand.
The daily results show that FHSA finds a better solution than the other versions of HSA. Indeed, it achieves a minimum daily gain of 187 $/day which is more than 68 000 $/year. Besides, the FHSA results reduce the transmission losses (a daily gain of approximately 70 MW) and the NOx emissions.
In order to demonstrate the performance of the proposed algorithms, a comparison for the power demand of 283.4 MW emerges between Harmony Search based algorithms and Genetic Algorithm [1], as is shown in table 6.
Table 6. Comparison results
|
|
Fuel cost ($/hr) |
Power loss (MW) |
NOx emission (ton/hr) |
|
Genetic Algorithm[1] |
824.9884 |
6.9661 |
0.2659 |
|
HSA |
881.131 |
3.913 |
0.204 |
|
IHSA |
883.329 |
3.958 |
0.204 |
|
GHSA |
885.757 |
3.812 |
0.203 |
|
FHSA |
877.110 |
2.635 |
0.204 |
From the results, it is obvious that the Harmony Search based algorithms are performing well in the solution of combined economic emission dispatch. Moreover, they obtain better compromises between cost optimization and emission minimization.
Conclusion
In this paper the Dynamic Economic-Environmental Dispatch problem is solved by different versions of Harmony Search Algorithm to minimize the fuel cost and NOx emissions.
Four harmony search based algorithms are implemented in ERELEC2 software that allows the user to resolve different types of problems one can meet in the field of power network optimization.
Satisfactory results are obtained by adapting harmony search based algorithms to six generators system and found that those results outperform some results in the literature.
The advantage of using ERELEC2 software to resolve the power network optimization problem is its simplicity in modelling and visualising all the results of economic and/or environmental dispatch.
Thus, the proposed software is a simple tool for the power industry to aid in curbing pollution and protecting our environment.
References
1. Bouktir T., Slimani L., Object-Oriented Economic Power Dispatch of Electrical Power System with minimum pollution using a Genetic Algorithm, J. Electrical Systems, 2005, 1-2, p. 19-34.
2. Geem Z.W., Kim J.H., Loganathan G.V., A New Heuristic Optimization Algorithm: Harmony Search, Simulation, 2001, 76(2), p. 60-68.
3. Geem Z.W., Improved Harmony Search from Ensemble of Music Players, International Conference on Knowledge-Based Intelligent Information and Engineering Systems, 2006, 4253, p. 86-93.
4. Mahdavi M., Fesanghary M., Damangir E., An improved harmony search algorithm for solving optimization problems, Applied Mathematics and Computation, 2007, 188(2), p. 1567-1579.
5. Omran M.G., Mahdavi M., Global-best harmony search, Applied Mathematics and Computation, 2008, 198(2), p. 643-656.
6. Battiti R., Brunato M., Mascia F., Reactive Search and Intelligent Optimization, Technical Report Università di Trento DIT-07-049, Available at: http://www http://reactive-search.org.
7. Benasla L., Belmadani A., Rahli M., Application of SUMT Method to Combine Economic and Emission Dispatch, Leonardo Journal of Sciences, 2008, 13, p. 122-132.
8. Kermanshahi B., Aizowa Y., Genetic algorithm for coordination of environmental and economy objectives in ELD problem, Journal of Electrical Science and Technology, 1996, p. 85-92.
9. Rahli M., Pirotte P., Optimal load flow using sequential unconstrained minimization technique (SUMT) method under power transmission losses minimization, Electric Power Systems Research, 1999, 52, p. 61-64.
10. Wallach Y., Even R., Calculations and programs for power systems network, Englewood Cliffs, Prentice-Hall, 1986.
11. Huang C.M., Yang H.T., Huang C.L., Bi-objective power dispatch using fuzzy satisfaction maximizing decision approach, IEEE Transactions on Power Systems, 1997, 12(4), p. 1715-1721.
12. ELGERD O.I., Electrical energy systems theory, Mc Graw.Hill Company, 1971.
13. Sudhakaran M., Slochanal M.R.S., Sreeran R., Chandrasekhar N., Application of refined genetic algorithm to combined economic and emission dispatch, IE (I) Journal-EL, 2004, 85, p. 115-119.
14. Kumarappan N., Mohan M.R., Hybrid genetic algorithm based combined economic and emission dispatch for utility system, ICISIP, 2004, p. 19-24.
15. Belmadani A., Benasla L., Rahli M., Etude d’un Dispatching Economique Environnemental par la méthode Harmony Search, ACTA Electrotehnica, 2009, 50, p. 44-48.
16. Belmadani A., Benasla L., Rahli M., A Fast Harmony Search Algorithm for Unimodal Optimization with Application to Power System Economic Dispatch, Search Algorithms and Applications, Prof. Nashat Mansour (Ed.), ISBN: 978-953-307-156-5, InTech, Available from: http://www.intechopen.com/books/ search-algorithms-and-applications/ a-fast-harmony-search-algorithm-for-unimodal-optimization-with-application-to-power-system-economic-, (2011).
17. Belmadani A., Benasla L., Rahli M., A Fast Harmony Search Algorithm for solving Economic Dispatch problem, Przeglad Elektrotchniczny, (Electrical Review), ISSN 0033-2097, R.86 Nr 3/2010, pp 274-278.