Dependence of Ionicity and Thermal Expansion Coefficient on Valence Electron Density in AIIBIVC2V Chalcopyrite Semiconductors
Amar BAHADUR1* and Madhukar MISHRA2
1 Department
of Physics, Kamla Nehru Institute of Physical and
Social Sciences, Sultanpur- 228 118 (U.P.),
2 Department
of Physics, Birla Institute of Technology and
Science, Pilani - 333 031 (Rajasthan),
E-mail(s): (1) abr.phys@gmail.com; (2) madhukar@bits-pilani.ac.in
* Corresponding author: Phone: +91- 9451431428
Abstract
A striking correlation has been found to exist between the free electron density parameter, average bond length, homoplar energy gap, heteropolar energy gap, ionicity and thermal expansion coefficient for AIIBIVC2V chalcopyrite semiconductors. The estimated values of these parameters are in good agreement with the available experimental values and theoretical findings. The electron density parameter data is the only one input data to estimate all above properties.
Keywords
Electron density parameter; Bond ionicity; Thermal expansion coefficient; Ternary chalcopyrite semiconductors.
Introduction
In recent years, ternary chalcopyrite semiconductors have attracted considerable attention because of their potential applications in the field of light emitting diodes, non-linear optics, photovoltaic devices and solar cells [1-4]. The solid solutions of these semiconductors have been used in electro-optic devices [5-7]. Their mixed crystals are being used for fabrication of detectors, lasers and integrated optic devices such as switches, modulators and filters etc. These chalcopyrites have many other practical applications in the areas of fiber optics, sensors and communication devices. In spite of their promising applications, some physical properties of these compounds have still not been significantly investigated. Frequent attempts have been made at understanding the crystal ionicity of these compounds. Phillips [8], Van Vechten [9-10], Levine [11] and other researchers [12-13] have developed various theories and calculated crystal ionicity for the case of simple compounds. Phillips and Van Vechten have calculated the homopolar and heteropolar contribution to the chemical bond in the binary crystals. Chemla [14] and several workers [15-16] have extended this theory to some complex crystals, neglecting the effect of noble metal d electrons. Levine [17] has extended Phillips and Van Vechten (PVV) theory of bond ionicity in case of various types of complex compounds considering the effect of d core electrons. It is clear form the Levine’s modifications and as well as PVV theory that the homopolar energy gap depends upon the nearest neighbor distance, while heteropolar energy gap is a function of nearest neighbor distance and the number of valence electron taking part in bond formation. Kumar et al. [18-19] have calculated these parameters in terms of plasmon energy because plasmon energy depends directly on the effective number of valence electrons in a compound. In all the above investigations, the ionicity has been evaluated in terms of nearest neighbor distance, valence and plasmon energy.
In recent years, various electronic and mechanical properties of ternary tetrahedral semiconductors have been explained using plasma oscillation theory [20-22], which leads to the fact that these physical properties depend directly on effective number of valance electrons and the density of the conduction electrons. The plasmon energy is related to the effective number of valence electrons as,
![]() (1)
(1)
where![]() is the
effective number of valence electrons,
is the
effective number of valence electrons, ![]() is
the charge,
is
the charge, ![]() is the mass of electron and
is the mass of electron and![]() is the plasmon energy is given by relation [23] as:
is the plasmon energy is given by relation [23] as:
![]() (2)
(2)
where, ![]() is
effective number of electrons taking part in plasma oscillation,
is
effective number of electrons taking part in plasma oscillation, ![]() is
the density and
is
the density and ![]() is the molecular weight of
compound. This equation is valid for free electron model but to a fairly good approximation
it can also be used for semiconductors and insulators. The valence electron
density is described by electron density parameter
is the molecular weight of
compound. This equation is valid for free electron model but to a fairly good approximation
it can also be used for semiconductors and insulators. The valence electron
density is described by electron density parameter ![]() which
also depends upon the density of the conduction electrons and effective number
of valence electrons according to relation [24],
which
also depends upon the density of the conduction electrons and effective number
of valence electrons according to relation [24],
![]() (3)
(3)
We, therefore, explore in the current work a new method for correlating electron density parameter with the crystal ionicity and thermal expansion coefficient for ternary chalcopyrite semiconductors. In the proposed approach, electron density parameter is the only input required for computation of the average bond length, homopolar energy gap, heteropolar energy gap, ionicity and thermal expansion coefficient.
Theory and Calculation
Average Bond Length, Homopolar Energy Gap, Heteropolar Energy Gap And Ionicity
The average bond length (d) is also related to the effective number of valence electrons, so there must be some correlation between bond length and electron density parameter. Using eqn. (1) and (3), we can express number of free electrons in terms of rs as-
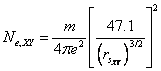 (4)
(4)
In tetrahedral semiconductors, the effective number of valence electrons Ne,XY can also be expressed in terms of individual bond properties as-
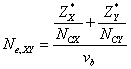 (5)
(5)
where,
![]() and
and![]() are
the number of valence electrons of the atom X and Y respectively,
in XY compounds.
The NCX , NCY and
NCZ are
coordination number of atoms and
are
the number of valence electrons of the atom X and Y respectively,
in XY compounds.
The NCX , NCY and
NCZ are
coordination number of atoms and ![]() is bond
volume. For AIIBIVC2Vsemiconductors,
NCA = NCB =
is bond
volume. For AIIBIVC2Vsemiconductors,
NCA = NCB = ![]() ,
,![]() and
and ![]() . Thus
for A-C and B-C bonds, eqn. (5) becomes-
. Thus
for A-C and B-C bonds, eqn. (5) becomes-![]() and
and
![]() , respectively. With the help
of these values and eqn. (4), we get following simple
correlation between average bond length and free electron density parameter for
, respectively. With the help
of these values and eqn. (4), we get following simple
correlation between average bond length and free electron density parameter for![]() and
and![]() bonds
as-
bonds
as-
![]() (6)
(6)
![]() (7)
(7)
The average energy gap![]() can be
separated into the homopolar and heteropolar
parts according to following relation:
can be
separated into the homopolar and heteropolar
parts according to following relation:
![]() (8)
(8)
which yield following relation for bond ionicity (fi):
![]() (9)
(9)
where, ![]() ,
,![]() are homopolar energy gap, ionic gap, respectively, given by
relations as:
are homopolar energy gap, ionic gap, respectively, given by
relations as:
![]() (10)
(10)
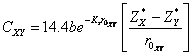 (11)
(11)
where dXY is distance between atoms X
and
Y, Ks
is
Thomas- Fermi momentum, ![]() ,
, ![]() is
Thomas-Fermi screening factor which is related to the effective number of free
electrons in compound and b is prescreening constant.
is
Thomas-Fermi screening factor which is related to the effective number of free
electrons in compound and b is prescreening constant.
With the help of eqn. (6) - (7) and (10), homopolar part of energy of individual bonds can be expressed in terms of free electron density parameter as:
![]() (12)
(12)
![]() (13)
(13)
The physical meaning of Eq. (11) is that ![]() is
given by the difference between the screened Coulomb potentials of atoms
is
given by the difference between the screened Coulomb potentials of atoms ![]() and
and ![]() having
core charges
having
core charges ![]() and
and ![]() . These
potentials are to be evaluated at the covalent radii
. These
potentials are to be evaluated at the covalent radii ![]() . Only
a small part of the electrons are in the bond, the rest screen the ion cores,
reducing their charge by the Thomas- Fermi screening factor
. Only
a small part of the electrons are in the bond, the rest screen the ion cores,
reducing their charge by the Thomas- Fermi screening factor ![]() , which
affects the chemical trend in a compound. This screening factor, as well as the
bond length, is related to the effective number of free electrons in a
compound. Also, the electron density parameter directly depends upon the
effective number of valence electrons. Thus, there must be some correlation
between the physical processes which involve the ionic contribution
, which
affects the chemical trend in a compound. This screening factor, as well as the
bond length, is related to the effective number of free electrons in a
compound. Also, the electron density parameter directly depends upon the
effective number of valence electrons. Thus, there must be some correlation
between the physical processes which involve the ionic contribution ![]() to
the average energy gap
to
the average energy gap ![]() and the electron density
parameter
and the electron density
parameter ![]() .
.
The expression for Thomas- Fermi momentum is given by relation as:
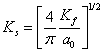 (14)
(14)
where, ![]() is Bohr
radius (0.529
is Bohr
radius (0.529![]() ) and
) and ![]() , the
Fermi wave vector given by relation as:
, the
Fermi wave vector given by relation as: ![]() . Using
eqn. (4), the Fermi wave vector can be expressed in
terms of
. Using
eqn. (4), the Fermi wave vector can be expressed in
terms of ![]() as:
as: ![]() and
accordingly Fermi- momentum becomes-
and
accordingly Fermi- momentum becomes-
![]() (15)
(15)
Using the values of Eq.
(15), the heteropolar energy can be expressed in
terms of ![]() as-
as-
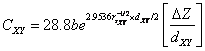 (16)
(16)
here, ![]() , is 3
and 1, for
, is 3
and 1, for ![]() and
and ![]() bond,
respectively, in AIIBIVC2V
semiconductors. The avergae value of prescreening
constant (b) has been taken as 1.3966 (Ref. 17) and 2.4516 (Ref. 17) for
bond,
respectively, in AIIBIVC2V
semiconductors. The avergae value of prescreening
constant (b) has been taken as 1.3966 (Ref. 17) and 2.4516 (Ref. 17) for
![]() and
and ![]() bond,
respectively. Using these values, we obtain expressions for heteropolar
energy gap for
bond,
respectively. Using these values, we obtain expressions for heteropolar
energy gap for ![]() and
and ![]() bond
as:
bond
as:
![]() (17)
(17)
![]() (18)
(18)
The ionicity
of ![]() and
and ![]() bonds
in AIIBIVC2V
semiconductors have been calculated using Eq. (9).
The ionicity of both bonds (
bonds
in AIIBIVC2V
semiconductors have been calculated using Eq. (9).
The ionicity of both bonds (![]() and
and ![]() ) exhibit a linear relationship
when plotted against electron density parameter. In fig. 1, we observe that in
plot of ionicty and electron density parameter, the
) exhibit a linear relationship
when plotted against electron density parameter. In fig. 1, we observe that in
plot of ionicty and electron density parameter, the ![]() bond
lie on line nearly parallel to the
bond
lie on line nearly parallel to the ![]() bond
and the ionicity trends in these bonds increases with
increasing electron density parameter. Based on above discussion, we propose
the following equation for the calcualation of the ionicity of ternary chalcopyrite semiconductors,
bond
and the ionicity trends in these bonds increases with
increasing electron density parameter. Based on above discussion, we propose
the following equation for the calcualation of the ionicity of ternary chalcopyrite semiconductors,
![]() (19)
(19)
where ![]() and
and![]() are
constants, The numerical values of these constants for
are
constants, The numerical values of these constants for ![]() and
and
![]() bonds are 0.4014 and
0.1651 and 0.265 and 0.365 respectively.
bonds are 0.4014 and
0.1651 and 0.265 and 0.365 respectively.
Table 1. Properties of AIICV bond in AIIBIVC2V compounds
|
Compounds |
Electron density parameter |
Average bond length |
Homopolar energy gap |
Heteropolar energy gap |
Ionicity |
|
|
|
Present work |
Levine [17] |
|
|||||
|
|
|
|
|
|
|||
|
ZnSiP2 |
2.12 |
2.38 |
4.653 |
4.557 |
0.4895 |
0.438 |
|
|
ZnGeP2 |
2.13 |
2.39 |
4.605 |
4.515 |
0.4902 |
0.442 |
|
|
ZnSnP2 |
2.15 |
2.42 |
4.459 |
4.388 |
0.4920 |
0.455 |
|
|
ZnSiAs2 |
2.20 |
2.46 |
4.245 |
4.200 |
0.4948 |
0.436 |
|
|
ZnGeAs2 |
2.21 |
2.48 |
4.168 |
4.133 |
0.4957 |
0.422 |
|
|
ZnSnAs2 |
2.24 |
2.51 |
4.061 |
4.038 |
0.4971 |
0.450 |
|
|
CdSiP2 |
2.28 |
2.56 |
3.854 |
3.852 |
0.4998 |
0.539 |
|
|
CdGeP2 |
2.28 |
2.56 |
3.862 |
3.859 |
0.4997 |
0.532 |
|
|
CdSnP2 |
2.31 |
2.59 |
3.755 |
3.762 |
0.5011 |
0.536 |
|
|
CdSiAs2 |
2.35 |
2.64 |
3.572 |
3.596 |
0.5034 |
0.553 |
|
|
CdGeAs2 |
2.35 |
2.64 |
3.565 |
3.590 |
0.5035 |
0.549 |
|
|
CdSnAs2 |
2.38 |
2.67 |
3.473 |
3.505 |
0.5047 |
0.553 |
|
Table 2. Properties of BIVCV bond in AIIBIVC2V compounds
|
Compounds |
Electron density parameter |
Average bond length |
Homopolar energy gap |
Heteropolar energy gap |
Ionicity |
|
|
|
Present work |
Levine [17] |
|
|||||
|
|
|
|
|
|
|||
|
ZnSiP2 |
1.85 |
2.25 |
5.304 |
2.705 |
0.2064 |
0.177 |
|
|
ZnGeP2 |
1.90 |
2.32 |
4.926 |
2.532 |
0.2090 |
0.219 |
|
|
ZnSnP2 |
2.04 |
2.49 |
4.156 |
2.171 |
0.2143 |
0.298 |
|
|
ZnSiAs2 |
1.93 |
2.35 |
4.779 |
2.464 |
0.2100 |
0.220 |
|
|
ZnGeAs2 |
1.97 |
2.41 |
4.501 |
2.334 |
0.2119 |
0.182 |
|
|
ZnSnAs2 |
2.10 |
2.56 |
3.870 |
2.033 |
0.2163 |
0.135 |
|
|
CdSiP2 |
1.84 |
2.25 |
5.346 |
2.724 |
0.2061 |
0.191 |
|
|
CdGeP2 |
1.91 |
2.33 |
4.909 |
2.524 |
0.2091 |
0.231 |
|
|
CdSnP2 |
2.04 |
2.49 |
4.152 |
2.169 |
0.2144 |
0.298 |
|
|
CdSiAs2 |
1.92 |
2.35 |
4.789 |
2.469 |
0.2099 |
0.234 |
|
|
CdGeAs2 |
1.98 |
2.42 |
4.436 |
2.304 |
0.2124 |
0.199 |
|
|
CdSnAs2 |
2.11 |
2.57 |
3.813 |
2.006 |
0.2167 |
0.148 |
|
Generalizing Eqs. (6)-(7), (12)-(13), (17), (18) and (19), the expression for average bond length, homoploar, heteropolar energy gap and ionicity can be written as:
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
where ![]() and
and
![]() are constants depending
upon bonds of compound. Form these Eqs., it follows that bond properties can be evaluated form
free electron density parameter. The free electron density parameter has been
calculated from eqn. (3). Using Eq.
(6)-(7), (12)-(13), (17), (18) and (19), we have calculated the average bond
length, homopolar gap, heteropolar
energy gap and bond ionicity for
are constants depending
upon bonds of compound. Form these Eqs., it follows that bond properties can be evaluated form
free electron density parameter. The free electron density parameter has been
calculated from eqn. (3). Using Eq.
(6)-(7), (12)-(13), (17), (18) and (19), we have calculated the average bond
length, homopolar gap, heteropolar
energy gap and bond ionicity for ![]() and
and
![]() bond in AIIBIVC2V
semiconductors and presented in Table-1 and 2, respectively. For comparison,
other estimates of these parameters are also presented. In most of compounds,
our calculated values are in good agreement with the earlier reported values
[17].
bond in AIIBIVC2V
semiconductors and presented in Table-1 and 2, respectively. For comparison,
other estimates of these parameters are also presented. In most of compounds,
our calculated values are in good agreement with the earlier reported values
[17].
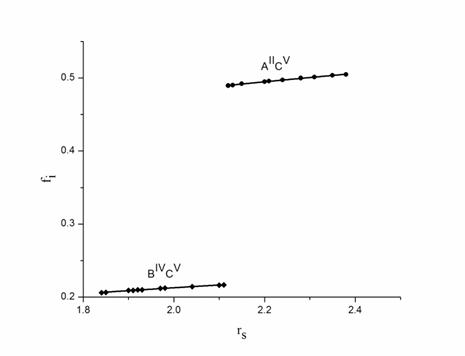
Figure 1. Plot of ionicity (fi) and electron density parameter (rs) for AIIBIVC2V chalcopyrite semiconductors. ● corresponds to the II-V bond and ♦ corresponds to IV-V bond in AIIBIVC2V chalcopyrite semiconductors. In this figure all data are taken from calculated values, which are presented in Table 1 and 2
Thermal Expansion Coefficient
Based on thermal expansion coefficient data, Neumann [25] has proposed following expression for the average thermal expansion coefficient for binary tetrahedral semiconductors:
![]() (24)
(24)
where A is
constant, Tm is melting temperature, d
is the bond length. The value of A is 0.021 for all tetrahedrally
coordinated compounds (AIV, AIIIBV, AIIBVI) as estimated
from a hard sphere model based on the diamond structure. The value ![]() is
equal to the bond length of diamond i.e.
is
equal to the bond length of diamond i.e.![]() . The
ternary chalcopyrites of general composition AIIBIVC2V can be
considered as similar to those of AIIBIV and AIIBVI. Thus,
Eq. (24) can also be reasonably used to describe the
thermal expansion coefficient of the ternary chalcopyrite. From Eq. (6) and (7), we get following relation between
. The
ternary chalcopyrites of general composition AIIBIVC2V can be
considered as similar to those of AIIBIV and AIIBVI. Thus,
Eq. (24) can also be reasonably used to describe the
thermal expansion coefficient of the ternary chalcopyrite. From Eq. (6) and (7), we get following relation between![]() and
and![]() as:
as:
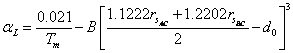 (25)
(25)
For AIIBIVC2V
chalcopyrite semiconductors, the values of B and![]() are 16.1
(
are 16.1
(![]() ) and 1.573
) and 1.573![]() , respectively [25]. Using Eq. (25), we
have calculated the thermal expansion coefficient for AIIBIVC2V,
ternary chalcopyrite semiconductors and presented in Table 3 along with
experimental data and theoretical findings.
, respectively [25]. Using Eq. (25), we
have calculated the thermal expansion coefficient for AIIBIVC2V,
ternary chalcopyrite semiconductors and presented in Table 3 along with
experimental data and theoretical findings.
Table 3. Thermal expansion coefficient of AIIBIVC2V compounds
|
Compounds |
Tm(K) [25-26] |
αL = (10-6K-1) |
||
|
Present work Eq. (25) |
Ref. [25] |
Exp. [25, 27] |
||
|
ZnSiP2 |
1643 |
6.15 |
|
6.3 |
|
ZnGeP2 |
1298 |
8.52 |
|
6.7 |
|
ZnSnP2 |
1203 |
6.57 |
|
3.2 |
|
ZnSiAs2 |
1369 |
5.99 |
5.3 |
|
|
ZnGeAs2 |
1148 |
7.62 |
6.7 |
1.0 |
|
ZnSnAs2 |
1048 |
5.80 |
4.5 |
2.3 |
|
CdSiP2 |
1393 |
5.83 |
7.0 |
7.2 |
|
CdGeP2 |
1073 |
9.00 |
|
6.1 |
|
CdSnP2 |
843 |
10.5 |
4.9 |
|
|
CdSiAs2 |
1120 |
6.16 |
5.0 |
|
|
CdGeAs2 |
938 |
8.19 |
|
6.0 |
|
CdSnAs2 |
871 |
5.56 |
|
4.7 |
Summary and Conclusion
The present relation may be considered to be first attempt to obtain simple correlations between free electron density parameter, average bond length, homopolar energy gap, heteropolar energy gap, ionicity and thermal expansion coefficient for ternary chalcopyrite semiconductors. These equations can be considered advantageous over others in the sense that it relates the electronic and thermal properties of semiconducting compounds with the free electron density parameter. The proposed relations yield not only satisfactory results, but also a comparison with the standard data provides a direct and precise check of the validity. Therefore, it is possible to predict the order of homopolar and heteropolar energy gap and the ionicity of semiconducting compounds from their free electron density parameter. The reasonable agreement between our calculated and previously known values of αL indicates that the proposed relations are both useful and accurate for estimating thermal properties for binary tetrahedral semiconductors. Hence, we conclude from present analysis that the ionicity and thermal properties in semiconducting compounds can be evaluated from density of valence electrons. In the proposed approach, the calculation is simple, fast and more accurate. The only information needed is electron density parameter; no other experimental values are required. It is natural to say that present approach can easily be extended to the other more complex crystals.
Acknowledgement
We are thankful to Dr. A.K. Srivastava (H.O.D., Department of Physics and Electronics,
K.N.I.P.S.S., Sultanpur, U.P.,
References
1.
Shay J. L., Wernick J. H., Ternary Chalcopyrite Semiconductors:
Growth, Electronic Properties and Applications,
2.
3. Medvedkin G. A., Voevdin V. G., Magnetic and optical phenomena in nonlinear optical crystals ZnGeP2 and CdGeP2, Jour. Opt. Soc. Am. B, 2005, 22, p. 1884-1898.
4. Jiang X., Lambrecht W. R. L., Electronic band structure of ordered vacancy defect chalcopyrite compounds with formula II-III2-VI4, Phys. Rev. B, 2004, 69, p. 035201-035209.
5. Narain S., Analysis of the Debye Temperature for ANB8–N Type Ionic and Partially Covalent Crystals, Phys. Stat. Solidi (b), 1994, 182, p. 273-278.
6. Neumann H., Simple theoretical estimate of surface energy, bulk modulus, and atomization energy of AIBIIICVI compounds, Cryst. Res. Tech., 1983, 18, p. 665-670.
7. Moss T. S., Relations between the Refractive Index and Energy Gap of Semiconductors, Phys. Stat. Solidi (b), 1985, 131, p. 415-427.
8. Phillips J. C., Dielectric Definition of Electronegativity, Phys. Rev. Lett., 1968, 20, 550-553; Ionicity of the Chemical Bond in Crystals, Rev. Mod. Phys., 1970, 42, p. 317-356.
9. Phillips J. C., Van Vechten J. A., Spectroscopic Analysis of Cohesive Energies and Heat of Formation of Tetrahedrally Coordinated Semiconductors, Phys. Rev. B, 1970, 2, p. 2147-2160; Nonlinear Optical Susceptibilities of Covalent Crystals, Phys. Rev., 1969, 183, p. 709-711.
10. Van Vechten J. A., Quantum Dielectric Theory of Electronegativity in Covalent Systems. I. Electronic Dielectric Constant, Phys. Rev., 1969, 182, p. 891-905.
11. Levine B. F., d-Electron Effects on Bond Susceptibilities and Ionicities, Phys. Rev. B, 1973, 7, p. 2591-2600.
12. Penn D. R., Wave-Number-Dependent Dielectric Function of Semiconductors, Phys. Rev., 1962, 128, p. 2093-2097.
13. Singh O. P., Gupta V. P., Comments on Levin's Modifications in the Phillips and Van Vechten Theory. d- Electron Effect on Ionicity, Phys. Stat. Solidi (b), 1986, 137, p. 97-101.
14. Chemla D. S., Dielectric Theory of Tetrahedral Solids: Application to Ternary Compounds with Chalcopyrite Structure, Phys. Rev. Lett., 1971, 26, p. 1441-1444.
15. Fischer J. E., Glickman M., Van Vechten J. A., Proceedings of the International Conference on the Physics of Semiconductors, Roma, Italy, 1976.
16. Neumann H., About the average bond ionicity in AIBIIICVI compounds, Cryst. Res. Tech., 1983, 18, p. 1391-1396.
17. Levine B. F., Bond susceptibilities and ionicities in complex crystal structures, J. Chem. Phys., 1973, 59, p. 1463-1487.
18. Kumar V., Prasad G. M., Electronic properties of ionic rocksalt crystals, Jour. Phys. Chem. Solids, 1989, 50, p. 899-901.
19. Srivastava V .K., Homopolar and heteropolar energy gaps in zincblende crystals, J. Phys. C: Solid State Phys., 1986, 19, p. 5689-5694.
20. Verma A. S., Bhardwaj S. R., Mechanical and optical properties of AIIBIVC2V and AIBIIIC2VI semiconductors, Phys. Stat. Solidi (b), 2006, 243, p. 2858-2863.
21. Kumar V., Srivastava A.K., Jha V., Bulk modulus and microhardness of tetrahedral semiconductors, Jour. Phys. Chem. Solids, 2010, 71, p. 1513-1520.
22. Gorai S. K., Mahto P., Plasmon energy, bulk modulus, electronic polarisability of AIBIIIC2VI and AIIBIVC2V ternary chalcopyrite semiconductors, Indian Jour. Phys. 2010, 84, p. 587-592.
23.
Phillips J. C., Bonds and Bands in Semiconductors,
24.
Ashcroft N.W., Mermin N. D.,
25. Neumann H., Trends in the thermal expansion coefficients of the AIBIIIC2VI and AIIBIVC2V chalcopyrite compounds, Kristall und Technik., 1980, 15, p. 849-957.
26. Garbato L., Rucci A., Microhardness of ternary chalcopyrite semiconductors, Phil. Mag., 1977, 35, p. 1685-1688.
27. Lide D.R. (Ed.), CRC Handbook of Chem. and Phys., 80th, CRC Press, 1999.