An Alternative Approach to Estimating the Bounds of the Denominators of Egyptian Fractions

 

Simon BROWN

 

School of Human Life Sciences, University of Tasmania, Locked Bag 1320, Launceston, Tasmania 7250, Australia.

E-mail: Simon.Brown@utas.edu.au

Phone: +61 3 63245400; Fax: +61 3 63243995

 

 

Abstract

Many fractions (a/b) can be expressed as the sum of three unit fractions. However, it remains to be shown (i) how the denominators of the unit fractions are to be calculated explicitly and (ii) how to determine whether a three unit fraction is sufficient to express a particular fraction. I show that the range of each of the denominators can be estimated using their sum (S) and product (P) and provide bounds on both S and P. The analysis presented also provides a means of identifying some of those cases for which more than three unit fractions is required.

Keywords

Denominator; Egyptian fraction; Inequality.

 

 

Introduction

 

Any fraction a/b, where 0 < a < b are integers, can be expressed as a sum of unit fractions. This approach had been used in ancient Egypt [1, 2] and are known as Egyptian fractions. How the Egyptians calculated the denominators of the unit fractions remains a matter of discussion [3, 4].

Many fractions can be written as a sum of just three unit fractions [5-10]

,

(1)

where 0 < p < q < r are integers. For example, only two unit fractions are needed if a = 2 [8], but these can be expressed as the sum of three unit fractions because any unit fraction can be expanded using 1/n = (1/(n + 1)) + (1/n(n + 1)). If a = 3 only three terms are needed [10] and it has been conjectured that this is also the case for a = 4 [11], a = 5 [5,6] and a = 6,7 [12,13]. However, some a/b can not be expressed as the sum of three unit fractions [14], for example 10/11 can not be represented in this way [13], so the general question remains an unsolved problem. Nevertheless, ‘almost all’ fractions can be expressed as the sum of three unit fractions [7] and for any a, the number of fractions required is less than (log b)˝ [9].

While a/b can often be expressed as the sum of three unit fractions (1), there are usually solutions for several values of p and there are often several (q, r) for a particular p [15]. The bounds on the denominators are

,

(2)

(3)

and

,

(4)

where

 and  

 

[15].  Of course, (2)-(4) provide a space within which to seek solutions of (1), but they do not represent a simple means of calculating the denominators. Moreover, since some a/b, such as 10/11, can not be expressed as the sum of three unit fractions [13,14], it would also be useful to be able to identify those a/b. Here I provide a means of calculating the denominators and make some progress towards identifying those a/b that can not be expressed as the sum of three unit fractions.

 

Calculating the denominators

 

The sum and product of the integer denominators are

S = p + q + r and P = p·q·r,

(5)

respectively. Each (S, P) corresponds to a single a/b, which is obvious, if S = p + q + r ≠ S´ = p´ + q´ + r´ and P = pqr ≠ P´ = p´q´r´, but consider two other cases:

(i)   S = S´, in which case p + q + r = p + (q + m) + (r – m), but P´ = p(q + m)(r – m) ≠ P.

(ii)  P = P´, in which case pqr = p(mq)(r/m), but S´ = p + mq + r/m and S ≠ S´ if m ≠ 1 and mq ≠ r.

Using (5), (1) can be written in terms of S and P

(6)

from which

(7)

(Figure 1). As S and P are integers, (7) implies that

 m = 1, 2, ...,

(8)

where gcd(x, y) is the greatest common divisor of x and y, and m is an integer in a range to be determined from the bounds of P estimated below. 

Eliminating one denominator (say r) from S and P yields a quadratic in the other two

.

(9)

Treating one root as known (say p), the roots of (9) give values for the other two denominators (q and r in this case)

(10)

from which S can be eliminated using (7)

.

(11)

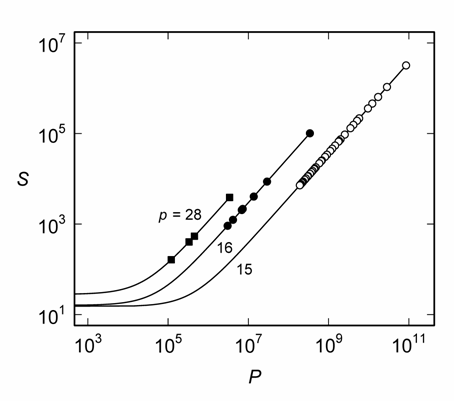
Figure 1. The relationship between S and P for a/b = 8/119 and selected values of p.  The points represent specific (p, q, r) for p = 15 (○), 16 (●) and 28 (■). The solid curves are given by (7) for p = 15, 16 and 28, as indicated.

 

The obvious problems with (10) and (11) are that (i) specific values of S and P are required and (ii) it is not known whether three terms in (1) are sufficient.  Moreover, when (1) applies there can be several (q, r)s for any given p, for example, for 8/119 there are 40 different solutions for p = 15 and 7 solutions for p = 16 (Figure 1), but none for p = 23.  This necessitates some insight into the ranges within which to search for the denominators, S and P.

 

 

Bounds on S and P

 

It is obvious from (5) that 3p < S < 3r and p3 < P < r3.  Alternatively, one could simply substitute the bounds of the denominators (2-4) into (5) to estimate the bounds of S and P.  However, a better approach is based on the mean inequality, since (1) is related to the harmonic mean (H) by H = 3b/a, which implies

(12)

These bounds can be improved using a cubic with roots p, q and r

(13)

which can be expressed in terms of S and P

(14)

The roots of f(x) are positive integers, which implies that the roots of f´(x) must also be real so S2 – 3(a/b)P > 0, from which an upper bound on P can be obtained, and since q and r must be real, an improved lower bound for P can be obtained from (11), so

(15)

which is sharper than (12).

A lower bound for S is obtained using (7) in (15)

(16)

and an upper bound for S can be obtained from the Schweitzer inequality [16]

(17)

which, using (1) and rearranging, yields

.

(18)

However, p/r < 1 and r/p < ar/b (1), so (18) becomes

(19)

and, for algebraic convenience, substituting Nickalls’ [17] bound on the roots of (14)

(20)

into (19) gives

.

(21)

Rearranging (21) yields

,

(22)

which is similar to (15) since the leading term is 35bS2/108a, but, after substituting (16), the RHS of (22) becomes

,

 

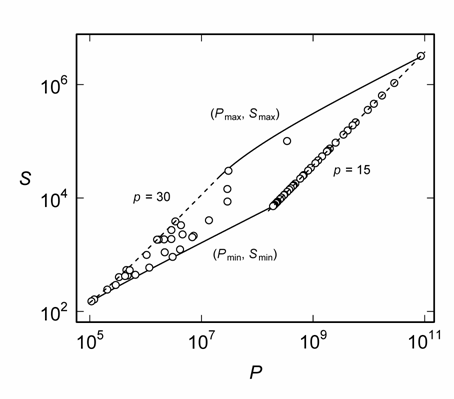
Figure 2. The region within which lie the solutions of (1) for a/b = 8/119.  The points represent specific (p, q, r) for p = 15, 16, ..., 30 (there are no solutions to (1) for p > 30).  The dashed curves are given by (7) for p = 15 or p = 30, as indicated.  The coordinates of the solid curves are (Pmin, Smin) and (Pmax, Smax), which are given by the lower and upper bounds, respectively, of (23) and (24) for p = 15, 16, ..., 30.

 

so

,

(23)

where the range of p is given by (2).  Similarly, the bounds of S are

.

(24)

Together, (23), (24) and (7) define an area within which the (S, P)s are located (Figure 2).

As is apparent from Figure 2, the number of solutions of (1) is small compared with the number of integer (S, P) coordinates within the area defined by (7), (23) and (24).  One might be tempted to speculate that there is a correlation between the number of solutions of (1) and the number of coordinates, which corresponds approximately to the area of the region, but there is no necessary correlation.  For example, the areas defined decline in the sequence a = 13, 14, 15 for b = 61 (Figure 3A). Of these, only 14/61 can be expressed as the sum of three unit fractions [13], although there are only two (p, q, r) = (5, 34, 10370) and (6, 16, 2928) as shown in Figure 3A.  Similarly, the areas defined for b = 71, 72 and 73 for a = 17 are similar (Figure 3B), but neither 17/71 nor 17/73 has any solutions [13], whereas 17/72 has the 14 solutions shown in Figure 3B.

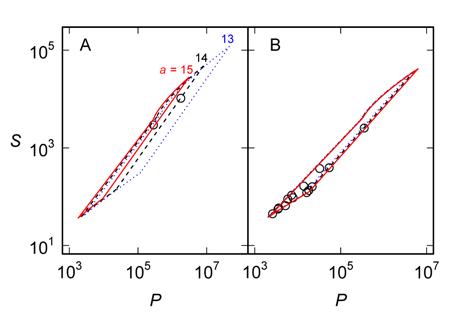
Figure 3. The regions defined by (7), (23) and (24) for a = 13, 14, 15 and b = 61 (A) and a = 17 and b =71, 72, 73 (B). The curves in (A) and (B), respectively, are a = 13 or b = 71 (∙∙∙∙∙∙), a = 14 or b = 72 (– – –), and a = 15 or b = 73 (——).  The points represent the only solutions for 14/61 (A) or 17/74 (B) and there are no solutions to (1) for the other cases.  Where appropriate, it was assumed that p varied in the range defined by (2).

 

 

Applications

 

Equations (7-8), (10-11) and (23-24) provide a systematic means of estimating p, q and r, either numerically or analytically.  For example, if a = 8, b = 119 and p = 28, then ap – b = 105 and bp2 = 93296, so (8) is P = 13328m for m = 1, 2, ....  However, (23) yields 1243449088/11025 < P < 126613974810400/5644800 so m ranges from 1243449088/(11025 × 13328) ≈ 9 to  126613974810400/(5644800 × 13328) ≈  1682 and S = 28 + (105/93296) × 13328m = 28 + 15m for m = 9, 10, ..., 1682.  Substituting these into (10) yields

(25)

from which the four solutions shown in Figure 1 for p = 28 are obtained (Table 1).

 

Table 1. Properties of the solutions of (1) for a/b = 8/119 and p = 28.  The four solutions given are those for which the specified m gives integral solutions (q and r) to (25).

m

Sum of

denominators (S)

Product of

denominators (P)

Calculated denominators

q

r

9

163

119952

51

84

25

403

333200

35

340

34

538

453152

34

476

256

3868

3411968

32

3808

 

Sierpiński [5] showed that

(26)

for n = 1, 2, ....  This expression yields the solution with the smallest S and P for the least p, but there are many others [15]. For example,

(27)

gives another (q, r) for the same p, whereas

(28)

is a solution for larger p. Naturally, (26) and (27) have different (S, P) coordinates, but they are both located on a line (7) through S = 2n + 1, whereas (28) is not.  All three lie (26-28) within the region defined by (7), (23) and (24) (Figure 4). It remains to obtain a general expression for the family of solutions of which (26-28) form a small part (Figure 4).

Taking (28) as an analytical example, a = 3, b = 6n +1 and p = 3n + 1, so ap – b = 3n + 2 and bp2 = (3n + 1)2(6n + 1).  As gcd(3n + 2, (3n + 1)2(6n + 1)) = 1, P = bp2m = (3n + 1)2(6n + 1)m (8) and S = 3n + 1 + (3n + 2)m (7).  Comparing the bounds of P (23) with P = (3n + 1)2(6n + 1)m, yields expressions corresponding to 8 ≤ m ≤ 1995, based on their partial fraction expansions. Substituting S and P into (10) yields an explicit expression for (q, r) in m and n

,

(29)

which implies the Diophantine equation . The only positive solution is , and substituting this into (29) yields the (q, r) given in (28). The Diophantine equation  implied in (10), or its equivalent in (11), may provide an indication as to whether a particular a/b can be expressed as (1): if there is no integer y, there can be no solution to (1).

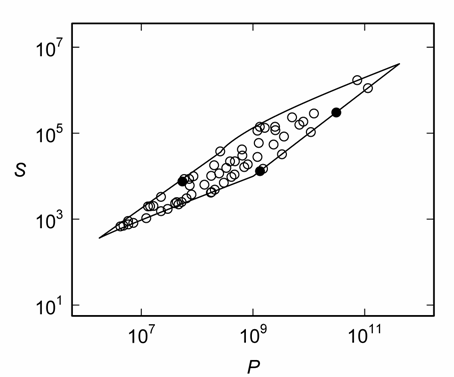
Figure 4. The region within which lie the solutions of (1) for a/b = 3/121.  The points (○) represent specific (p, q, r) for p = 41, 42, ..., 66 (there are no solutions to (1) for p > 66).  The three filled points (●) correspond to p = 2n + 1 (26-27) and p = 3n + 1 (28) for n = 20.  The bounds are given by (7), for p = 41 or p = 66, and (23) and (24) for p = 41, 42, ..., 66.

 

 

Conclusions

 

The sum (S) and product (P) of the denominators of (1) is linearly related to (7) and can be used to calculate the denominators (10-11). The bounds of P (23) and S (24) and a systematic means of calculating P (8) facilitate the efficient estimation of denominators. The method is useful in both numerical and analytical problems.

 

 

References

1.      Neugebauer O., The exact sciences in antiquity. New York, Dover Publications, Inc., 1969.

2.      Clagett M., Ancient Egyptian science: a source book. III. Ancient Egyptian mathematics. Philadelphia, American Philosophical Society, 1999.

3.      Abdulaziz A. A., On the Egyptian method of decomposing 2/n into unit fractions, Historia Mathematica, 2008, 35, p. 1-18.

4.      Dorsett C., A solution for the Rhind papyrus unit fraction decompositions, Texas College Mathematics Journal, 2008, 5(1), p. 1-4.

5.      Sierpinski W., Sur les décompositions de nombres rationnels en fractions primaires, Mathesis, 1956, 65, p. 16-32.

6.      Sierpinski W., Elementary theory of numbers. Warsaw, Panstwowe Wydawn Naukowe, 1964.

7.      Vaughan R. C., On a problem of Erdös, Straus and Schinzel, Matematika, 1970, 17, p. 193-198.

8.      Culpin D., Griffiths D., Egyptian fractions, Mathematical Gazette, 1979, 63(423), p. 49-51.

9.      Vose M. D., Egyptian fractions, Bulletin of the London Mathematical Society, 1985, 17, p. 21-24.

10.    Hagedorn T. R., A proof of a conjecture on Egyptian fractions, American Mathematical Monthly, 2000, 107(1), p. 62-63.

11.    Erdős P., Az 1/x1 + 1/x2 + ... + 1/xn = a/b egyenlet egész számú megoldásairól, Matematikai Lapok, 1950, 4, p. 192-210.

12.    Aigner A., Brüche als Summe von Stammbrűchen, Journal für die reine und angewandte Mathematik, 1964, 214/215, p. 174-179.

13.    Webb W. A., Rationals not expressible as a sum of three unit fractions, Elemente der Mathematik, 1974, 29(1), p. 1-6.

14.    Yamamoto K., On a conjecture of Erdös, Memoirs of the Faculty of Science, Kyushu University, 1964, 18(2), p. 166-167.

15.    Brown S., Bounds of the denominators of Egyptian fractions, World Applied Programming, 2012, 2(9), p. 425-430.

16.    Schweitzer P., Egy egyenlőtkenség az aritmetíkai kőzépértékről, Mathematikai és Physikai Lapok, 1914, 23, p. 257-261.

17.    Nickalls R. W. D., A new bound for polynomials when all the roots are real, Mathematical Gazette, 2011, 95(534), p. 520-526.
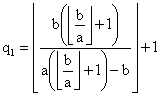
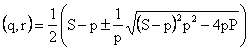
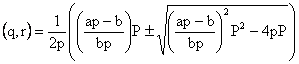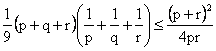
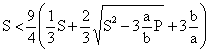