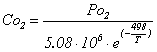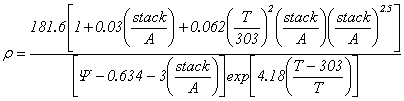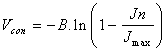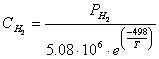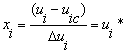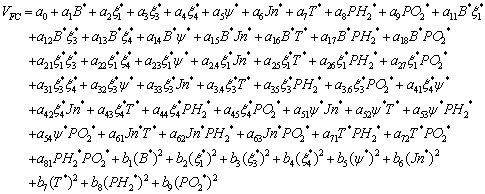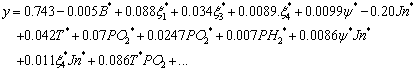A Central Composite Face-Centered Design for Parameters Estimation of PEM Fuel Cell Electrochemical Model
Khaled MAMMAR1,* and Abdelkader CHAKER2
1 Department of Electrical Engineering, University of Bechar, Bp 417,Bechar, Algeria
2 Department of Computers and Informatics, Faculty of Electrical Engineering and Informatics , Laboratory of Electrical network, E.N.S.E.T, E.N.S.E.T, B.P 1742 El M'naouar, Oran, Algeria,
E-mail: mammar.univ.dz@gmail.com
*Corresponding author: Phone: +213663539546
Abstract
In this paper, a new approach based on Experimental of design methodology (DoE) is used to estimate the optimal of unknown model parameters proton exchange membrane fuel cell (PEMFC). This proposed approach combines the central composite face-centered (CCF) and numerical PEMFC electrochemical. Simulation results obtained using electrochemical model help to predict the cell voltage in terms of inlet partial pressures of hydrogen and oxygen, stack temperature, and operating current. The value of the previous model and (CCF) design methodology is used for parametric analysis of electrochemical model. Thus it is possible to evaluate the relative importance of each parameter to the simulation accuracy. However this methodology is able to define the exact values of the parameters from the manufacture data. It was tested for the BCS 500-W stack PEM Generator, a stack rated at 500 W, manufactured by American Company BCS Technologies FC.
Keywords
Fuel cell; PEMFC Polymer-electrolyte fuel cell; Electrochemical model; Modelling and Simulation; Design of Experimental (DoE); Central composite face-centered (CCF).
Introduction
In recent years, with the problems of energy shortage and environment concerns, renewable and clean energy became more and more popular, one of the alternative sources of electric power is fuel cell. It is the clean energy, without any harmful emissions to the environment, and has high power density [2]. Proton Exchange Membrane (PEM) fuel cell is one kind of fuel cells that can work in a comparatively high efficiency and low temperature condition. It is one of the promising technologies for alternative power source of residential power generation in future.
A PEMFC converts the chemical energy of a fuel, just as the hydrogen H2, and an oxidizer, just as the oxygen O2, in electrical energy. The outline of a typical PEMFC is illustrated in Fig. 1 [2]. On one side of the cell, referred to as the anode, the fuel is supplied under certain pressure. The fuel for this model is the pure gas H2, although other compositions of gases can be used. In these cases, the hydrogen concentration should be determined in the mixture. The fuel spreads through the electrode until it reaches the catalytic layer of the anode where it reacts to form protons and electrons, as shown below in the reaction given in Equation (1) [1]-[9]:
|
H2 +
1/2 O2 |
(1) |
In order to get an electric current out of this reaction, hydrogen oxidation and oxygen reduction are separated by a membrane, which is conducting protons from the anode to the cathode side. The semi reactions on both electrodes are
|
H2
|
(2) |
|
O2 + 4
e- |
(3) |
While the protons are transported through the membrane, electrons are carried by an electric circuit in which their energy can be used. This process is shown in figure 1.
Modelling of fuel cells is getting more and more important as powerful fuel cell stacks are getting available and have to be integrated into power systems. In this paper a semi empirical model was proposed. This model includes the electrochemical and fluid dynamic aspects of chemical reactions inside the fuel-cell stack. In addition, voltage losses due to ohmic, activation, and concentration losses are accounted for. Furthermore, this PEMFC model was optimized by design of experimental methodology from manufacture data. For this a central composite face-centered (CCF) of Design of Experiments DoE method has been used to determine the optimum parameters of PEM fuel cell electrochemical model.
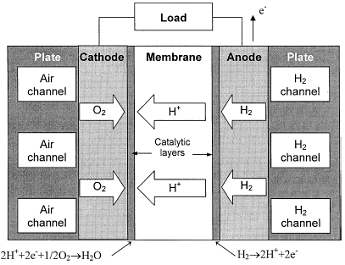
Figure 1. Basic Fell Cell Operation
Fuel Cell Model Formulation
In [2] - [4] a performance model for a proton exchange membrane (PEM) fuel cell stack was previously developed. The model incorporated both the mechanistic and empirical properties to describe the electrochemical phenomena of combining oxygen and hydrogen over a platinum catalyst to produce an electrical current and water. The previous model predicted the cell voltage in terms of inlet partial pressures of hydrogen and oxygen, stack temperature, and operating current. The cell voltage was defined as
|
VFC = ENenst - Vact - Vohm - Vconc |
(4) |
In Eq. (4), ENenst is the thermodynamic potential of the cell and its represents reversible voltage; Vact is the voltage drop due to the activation of the anode and of the cathode; Vohm is the ohmic voltage drop, a measure of the ohmic voltage drop associated with the conduction of the protons through the solid electrolyte and electrons through the internal electronic resistances; Vconc represents the voltage drop resulting from the concentration or mass transportation of the reacting gases [3]. The first term of Eq. (4) represents the FC open circuit voltage, while the three last terms represent reductions in this voltage to supply the useful voltage of the cell, for a certain operating condition. Each one of the terms in Eq. (4) can be calculated by the following equations [3]:
|
|
(5) |
where PH2 and PO2 while they are the partial pressures of hydrogen and oxygen (atm), respectively, T the cell operation temperature (K):
|
|
(6) |
where Istack is the cell operating current (A), and the ξi ’s represent parametric coefficients for each cell model, whose values are defined based on theoretical equations with kinetic, thermodynamic, and electrochemical foundations [4]. Co2 is the concentration of oxygen in the catalytic interface of the cathode mol/cm, determined by:
|
|
(7) |
|
|
(8) |
where Rc represents
the resistance to the transfer of protons through the membrane, usually
considered constant and: ![]() with
with ![]() : is the
specific resistivity of the membrane for the electron flow (cm), A is
the cell active area (cm) and l is the thickness of the membrane (cm),
which serves as the ectrolyte of the cell. The following numeric expression for
the resistivity of the Nafion membranes is used [3]:
: is the
specific resistivity of the membrane for the electron flow (cm), A is
the cell active area (cm) and l is the thickness of the membrane (cm),
which serves as the ectrolyte of the cell. The following numeric expression for
the resistivity of the Nafion membranes is used [3]:
|
|
(9) |
where ![]() the term is the specific resistivity (Ώ/ cm) at no current and at 30°C [3];
the term is the specific resistivity (Ώ/ cm) at no current and at 30°C [3];
|
|
(10) |
where B (V) is a parametric coefficient, which depends on the cell and its operation state, and Jn represents the actual current density of the cell (A/cm).
The values used for the parameters of fuel cell models are primarily based on manufacturing data and laboratory experiments. However, some aspects of PEMFC operation are still difficult to model accurately and some processes are proprietary of the manufacturers. The disagreements between measurements and calculations arise because of uncertainties stemming not only from experimental measurements, but also from ill-defined parameters [6].
The relative importance of the physical and electrochemical processes occurring in a fuel cell can be evaluated using Factorial Designs methodology. Such analysis is conducted in this paper using a fuel cell electrochemical model and data from a BCS500W PEMFC stack which is available in the literature, manufactured by the company BCS Technology [1, 4].
CCF Design of Experiment
A Design of Experiment (DoE) is a structured, organized method for determining the relationship between a number of factors affecting a process and the output of that process. Regardless of the domain of application, this methodology is useful for three objectives: screening, optimization, and robustness testing. Employed at the beginning of the investigation of a new application, screening experiments are commonly designed to explore many factors, in order to evaluate their effects on the responses. It also makes it possible to obtain the best possible precision on the modeling of results and thereafter the optimization of the process.
In the present section A CCF design from DoE was employed to determine the optimal conditions for the critical factors. This design is a kind of central composite design (CCD), in which the axial points are placed on the face centers of the cube; therefore, each factor has only three levels instead of five in CCD. With such cubical design, one or two center runs are sufficient to produce a reasonable stability of prediction variance [10]
Definition of Variation Intervals of the Factors
Before to use CCF design methodology, we first have to determine the maximum and minimum levels of each factor. This step is important because we have to define the field of variation of each factor, inside whose analysis and conclusions of the modeling will be valid [10].
In this study the CCF Design methodology is used to evaluate the respective impacts of
parameters model (such B, ξ1 (Xi1), ξ3 (Xi3), ξ4 (Xi4), ![]() (Psi), and physical control parameters (such as current density Jn(A/cm2),
stack temperature T(K), stack temperature, gas pressures (atm)) on the
FC operation Table 1
(Psi), and physical control parameters (such as current density Jn(A/cm2),
stack temperature T(K), stack temperature, gas pressures (atm)) on the
FC operation Table 1
Note: ξ2 is not impact of parameters it was calculated with relationship:
|
|
(11) |
![]() is the concentration of hydrogen in the catalytic interface of the
anode mol/cm, determined by:
is the concentration of hydrogen in the catalytic interface of the
anode mol/cm, determined by:
|
|
(12) |
Table 1. Factors
|
Factors |
Description |
Low |
High |
|
B |
(semi-empirical coeff. V) |
0.0144 |
0.0176 |
|
Xi1(ξ1) |
(parametric coefficient) |
-1.0430 |
-0.8532 |
|
Xi3 (ξ3) |
(parametric coefficient).10-4 |
6.84 |
8.36 |
|
Xi4 (ξ4) |
(parametric coefficient).10-5 |
-2.123 |
-1.737 |
|
Psi( |
(parametric coefficient) |
15 |
24 |
|
Jn |
current density (A/cm2 |
0.01 |
0.4219 |
|
T |
FC temperature, k |
288 |
3.70 |
|
PH2 |
(H2 partial pressure, atm) |
1.0 |
3.0 |
|
PO2 |
(O2 partial pressure, atm) |
1.0 |
3.0 |
We use CCF design with nine factors [7, 8].With such models, the response of the process is expressed their according to the factors ui (i = 1..., e):
|
|
(13) |
where c0, ci, and cij are calculated coefficients. A normalized centered value can be defined for each factor as follows:
|
|
(14) |
where:
|
|
(15) |
With these notations, the function of response becomes:
|
|
(16) |
where xi can obviously take only the values: −1 (for minimal input value ximin), +1 (for maximal input value ximax)and 0 (for center input value xic).
For the nine factors considered in the present study, i.e. x1= B*, x2= ξ1*, x3= ξ2*, x3= ξ3*, x4= ξ4*, x5=ψ*, x6=Jn*, x7=T*, x8=PH2*, x9=PO2*, the linear model will take the following form:
|
|
(17) |
Matrix of the full factorial design
Matrix of CCF design of such a design with nine factors is given in Table 2 (were (1), (−1) and (0) designate maximal, minimal and center values of factors.) developed with Software MODDE 5.0 (Umetrics AB, Umea, Sweden) allows creation and analyzes of experimental designs; the program assists the user for analysis of the results and prediction of the responses [10]-[12]. It calculates the coefficients of the factors and allows modeling and optimization of the process. Obtained results according to matrix are presented in Table 3 were the response y=VFC was calculated from the electrochemical model by relationship given in (4). Fig. 2 shows the results of the response of y =VFC calculated by electrochemical model.
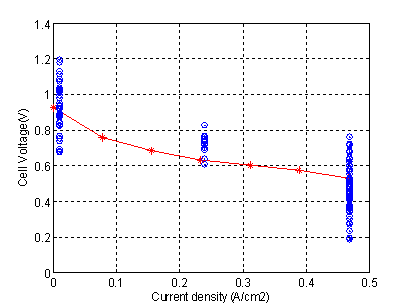
Figure 2. Cell polarization o simulated cell voltage (*BCS 500-W manufacture data)
Figure 3 represents significant effect of the model shows that the current density is the most influent factor on the cell voltage of PEM fuel cell, because it has a high effect coefficient compared to other factors.
We also notice that the influences of the all interaction are negligible except which exists between (Jn and Xi4, Psi and Jn) .The mathematical model of the response (Cell voltage) is linear with significant interactions, given by:
|
|
(18) |
Table 2. Matrix of CCF design with nine factors
|
N |
B* |
Xi1* |
Xi3* |
Psi* |
Xi4* |
Jn* |
T* |
PH2* |
PO2* |
|
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|
2 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
1 |
-1 |
|
3 |
-1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
1 |
|
4 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
-1 |
|
... |
|
|
|
|
|
|
|
|
|
|
132 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
133 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
134 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
... |
|
|
|
|
|
|
|
|
|
|
148 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
149 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
148 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Evaluation of quality of the mathematical model
The quality of the obtained mathematical model can be evaluated by two statistical criteria which are given directly by software MODDE 5.0 to check experimental (R2 criterion) and predictive (Q2 criterion) quality of the mathematical model. When values of R2 and Q2 are close to the unit, the model is considered as good and can be used for optimization and prediction [11]. As values of these two criteria, according to the model given by equation (15), are respectively R2 = 0.999 and Q2 = 0.943 the model can thus be used to predict and optimize the process.
Table 3. Results of the tests of CCF
|
No |
B |
Xi1 |
Xi3 |
psi |
Xi4 |
Jn |
T |
PH2 |
PO2 |
VFC |
|
1 |
0.0144 |
-1.0428 |
6.84 |
15 |
-2.123 |
0.01 |
288 |
1 |
0.1 |
0.753961 |
|
2 |
0.0176 |
-1.0428 |
6.84 |
15 |
-2.123 |
0.01 |
288 |
3.05 |
0.1 |
0.767734 |
|
3 |
0.0144 |
-0.8532 |
6.84 |
15 |
-2.123 |
0.01 |
288 |
1 |
3 |
1.07379 |
|
4 |
0.0176 |
-0.8532 |
6.84 |
15 |
-2.123 |
0.01 |
288 |
3.05 |
3 |
1.08756 |
|
. . |
|
|
|
|
|
|
|
|
|
|
|
132 |
0.016 |
-0.8532 |
7.6 |
19,5 |
-1.93 |
0.23925 |
329 |
2.025 |
1.55 |
0.829 |
|
133 |
0.016 |
-0.948 |
6.84 |
19,5 |
-1.93 |
0.23925 |
329 |
2.025 |
1.55 |
0.767928 |
|
134 |
0.016 |
-0.948 |
8.36 |
19,5 |
-1.93 |
0.23925 |
329 |
2.025 |
1.55 |
0.700473 |
|
135 |
0.016 |
-0.8532 |
7.6 |
19,5 |
-1.93 |
0.23925 |
329 |
2.025 |
1.55 |
0.829 |
|
. . |
|
|
|
|
|
|
|
|
|
|
|
148 |
0.016 |
-0.948 |
7.6 |
19,5 |
-1.93 |
0.23925 |
329 |
2.025 |
1.55 |
0.7342 |
|
149 |
0.016 |
-0.948 |
7.6 |
19,5 |
-1.93 |
0.23925 |
329 |
2.025 |
1.55 |
0.7342 |
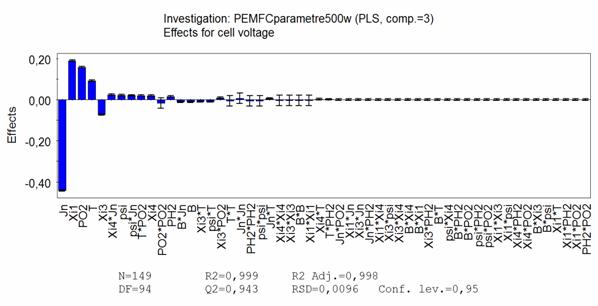
Figure 3. CCF effect estimation on cell voltage
Optimization of the Parameters
The objective of optimization is to find the parameters model of proton exchange membrane (PEM) given in
section 2 (such B, ξ1 (Xi1), ξ3 (Xi3), ξ4 (Xi4), ![]() (Psi) from manufacture and physical control parameters
of FC operation given in Table4.
(Psi) from manufacture and physical control parameters
of FC operation given in Table4.
The Optimum of the parameters predicted by the mathematical model (CCF Design methodology) developed with Software MODDE (fig 4) are:
B=
0.0167 V, ξ1= -0.948, ξ3=7.752∙10-5, ξ4 =-1.93
∙10-4 and ![]() =19.5
=19.5
Table 4. Manufacture of the 500-W BCS stack [1]
|
Parameters |
Values |
Parameters |
Values |
|
N |
32 |
RC |
0.0003 Ω |
|
T |
333K |
Imax |
30 A |
|
A |
64 cm2 |
Jmax |
0.469 A/cm2 |
|
L |
178 μm |
Jn |
0.2325A/cm2 |
|
PO2 |
0.2 atm |
Vn |
0.63 V/cell |
|
PH2 |
1atm |
|
|
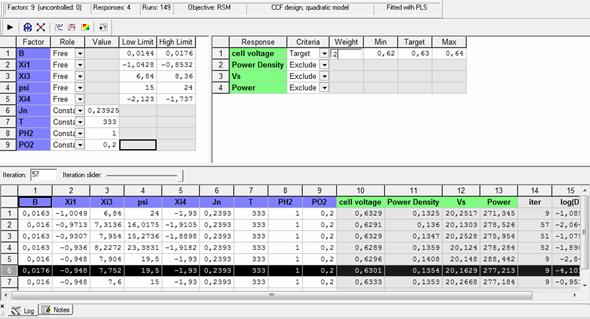
Figure 4. Optimum of the parameters predicted by MODDE Software
Simulation results
For validation, a model of 500 W BSC stack was simulated, which was fed with gases H2 and O2, using the membrane Nafion 117. The parameters used for this simulation are predicted by Factorial Design methodology (Software MODDE 5.0) shown in fig 3 and also presented in Table 4.
The simulation results of the PEM 500 W BCS stack fuel cell are represented in Fig. 5 and 6:
o Fig. 5 shows that a typical PEMFC cell voltage response surface, with simultaneous changes in the inlet partial pressure of hydrogen and current at a constant stack temperature of 70°C and compared to the manufacturer data
o Fig. 6 shows that a typical PEMFC cell voltage response surface, with simultaneous changes in the inlet temperature and current at a PH2=1atm with and compared to the manufacturer data.
The simulated results present a good agreement with the real data, except at the very beginning.
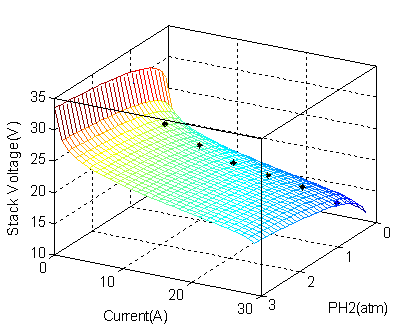
Figure 5. Typical PEMFC cell voltage response surface with simultaneous changes in the inlet partial pressure of hydrogen and current at a constant stack temperature of 70°C (*BCS 500-W manufacture data )
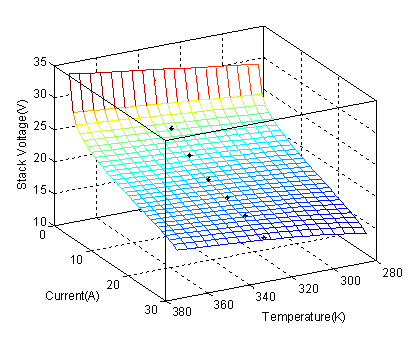
Figure 6. Typical PEMFC cell voltage response surface with simultaneous changes in the inlet stack temperature and current (*BCS 500-W manufacture data)
Conclusion
The optimization of the operating parameters affecting the performance of PEMFC and obtaining related data are very important in various applications, and especially for fuel cell producers to validate and improve their models. In the present study, a central composite face-centered (CCF) of Design of Experiments DoE method has been used to determine the optimum parameters of PEM fuel cell electrochemical model. A CCF design, at two levels and nine factors, has been carried out in order to analyze model of fuel cell. The obtained results show that optimized DoE can successfully predict the exact values parameter of fuel cell model from manufacture.
References
1. BCS Technology Co., Data sheet for a 500 W FC stack, 2001.
2. Jeferson M. C, Felix A. F., Luciane N., An Electrochemical-Based Fuel-Cell Model Suitable for Electrical Engineering Automation Approach, IEEE Transactios on Industrial Electronics, Octobr 2004, 51(5)
3. Correa J., Farret F., Canha L., An analysis of the dynamic performance of proton exchange membrane fuel cells using an electromechanical model, IEEE Industrial Electronics Conference IECON01, 2001, p. 141-146.
4. Naga S. G., Subrahmanyam T., Dharma V.R., Parametric sensitivity analysis of PEM fuel cell electrochemical Model, International Journal of Hydrogen Energy Science Direct 2011, article in press I-7.
5. Suleyman K., Levent A., Optimization of parametric performance of a PEMFC, International Journal of Hydrogen Energy Science Direct 2007, vol 32, p. 4418 – 4423
6. Outeiro M.T., Chibante R., A.S. Carvalhoc A.S., Almeida A.T., A parameter optimized model of a Proton Exchange Membrane fuel cell including temperature effects, Journal of Power Sources 2008, 185, p. 952–960
7. Mammar K., Chaker A., “Fuzzy logic -based control of power of PEM fuel cell system for residential Application”, Leonardo Journal of Sciences, January-June 2009, Issue 14, p. 147-166
8. Mammar K., Tahour A., Chaker A., Active and Reactive Power Control of Fuel Cell System Using a Neural Network Model and Fuzzy Logic Controller, International Review of Automatic Control (Theory and Applications) - May 2010 - Papers.
9. Eriksson L., Johansson E., Kettaneh N., Wikstöm C., Design of Experiments, Principles and Applications, Umetrics, 2009
10. Hicks C. R., Turner K.V., Fundamental Concepts in the Design of Experiments, Oxford, U.K.: Oxford Univ. Press, 1990.
11. R. K. Roy, “Design of the Experiments Using Taguchi Approach”. 16 Steps to Product and Process Improvement. New York: Wiley, 2001.
12. Thomas P., Acworth GA., Modern Experimental Design, 2007 by John Wiley & Sons, Inc. All rights reserved.