Economic Dispatch Problem using Bat Algorithm

Yamina Ahlem GHERBI ^1*, Hamid BOUZEBOUDJA ¹ and Fatiha LAKDJA²

¹ Electro technical Department, Faculty of Electrical Engineering, USTO, Oran, Algeria

² Intelligent Control and Electrical Power System Laboratory, Djillali Liabès University of Sidi-Bel-Abbes, Algeria

E-mails: aygherbi@yahoo.fr (YAG); hbouzeboudja@yahoo.fr (HB); flakdja@yahoo.fr (FL)

^* Corresponding author: Fax: 213 48 61 03 22

Abstract

A BAT algorithm to solve the economic dispatch problem is presented in this paper. The modern power system has become very complex in nature with consumption of the electric power which is in rise progression and this tendency increases with the industrialization and the growth of the population. Moreover, one loss of alimentation can cause the interruption of the various production processes, and in front of consumers who become increasingly demanding by wanting more energy and better quality, the companies of production of electrical energy must thus ensure the regular provisioning of this request, and without interruption, but these requirements compromise the cost of generation. Application of BAT algorithm in this paper is based on mathematical modeling to solve economic dispatch problems by a single equivalent objective function. The algorithm is tested on 6-unit system. BAT algorithm is easy to implement and better than other algorithms in terms of accuracy and efficiency.

Keywords

Bat Algorithm; Economic Dispatch; Optimization Methods; Metaheuristic.

Introduction

Economic dispatch (ED) is the operation of generation to produce energy at the lowest cost by fulfilling the demand within several limits. This is not an easy task since there are a lot of factors need to be considered especially in the large interconnected power systems. The primary objective of ED is to schedule the committed generating units output so as to meet the required load demand at minimum cost satisfying all unit and system operational constraints [1].

Various conventional methods like Bundle method, nonlinear programming, mixed integer linear programming, dynamic programming, quadratic programming, Lagrange relaxation method, network flow method, direct search method reported in the literature are used to solve such problems [1].

Practically, ED problem is nonlinear, non-convex type with multiple local optimal points due to the inclusion of valve point loading effect, multiple fuel options with diverse equality and inequality constraints.

Conventional methods have failed to solve such problems as they are sensitive to initial estimates and converge into local optimal solution and computational complexity [1].

Biology-inspired metaheuristic algorithms have recently become the forefront of the current research as an efficient way to deal with many NP-hard combinatorial optimization problems and non-linear optimization constrained problems in general [2]. These algorithms are based on a particular successful mechanism of a biological phenomenon of Mother Nature in order to achieve optimization, such as the family of honey-bee algorithms, where the finding of an optimal solution is based on the foraging and storing the maximum amount of flowers’ nectar [2]. A new algorithm that belongs in this category of the so-called nature inspired algorithms is the bat algorithm which is based on the echolocation behavior of bats [2].

In this research paper we present how the BAT algorithm can be used to solve the economic dispatch optimization problem. The effectiveness of proposed algorithm is demonstrated using six generating unit test system.

Formulation of the Economic Load Dispatch Problem

Economic Dispatch

The objective of economic load dispatch of electric power generation is to schedule the committed generating unit outputs so as to meet the load demand at minimum operating cost while satisfying all units and operational constraints of the power system. The economic dispatch problem is a constrained optimization problem and it can be mathematically expressed as follows:

(1)

where F_T: total generation cost (Rs/hr) n: number of generators P_n: real power generation of n^th generator (MW) F_n(P_n): generation cost for P_n Subject to a number of power systems network equality and inequality constraints [4]. These constraints include:

System Active Power Balance

For power balance, an equality constraint should be satisfied. The total power generated should be the same as total load demand plus the total line

(2)

where P_D: total system demand (MW) P_L: transmission loss of the system (MW)[4].

Generation Limits

Generation output of each generator should be laid between maximum and minimum limits. The corresponding inequality constraints for each generator are

Pn,min ≤ Pn ≤ Pn,max

(3)

where P_n,min: minimum power output limit of nth generator (MW) P_n,max: maximum power output limit of nth generator (MW) The generation cost function F_n(P_n) is usually expressed as a quadratic polynomial:

(4)

where a_n, b_n and c_n are fuel cost coefficients [4].

Network Losses

Since the power stations are usually spread out geographically, the transmission network losses must be taken into account to achieve true economic dispatch. Network loss is a function of unit generation. To calculate network losses, two methods are in general used.

One is the penalty factors method and the other is the B coefficients method. The latter is commonly used by the power utility industry. In the B coefficients method, network losses are expressed as a quadratic function:

(5)

where B_mn constants are called B coefficients or loss coefficients [4].

Bat Algorithm

Bats are fascinating animals. They are the only mammals with wings and they also have advanced capability of echolocation [7]. Most of bats use echolocation to a certain degree; among all the species, microbats are famous example as microbats use echolocation extensively, while megabats do not [7]. Microbats use a type of sonar, called echolocation, to detect prey, avoid obstacles, and locate their roosting crevices in the dark. If we idealize some of the echolocation characteristics of microbats, various bat-inspired algorithms or bat algorithms can be developed. For simplicity, in our approach, the following approximate or idealized rules were used:

· All bats use echolocation to sense distance, and they also know the difference between food/prey and background barriers.

· Bats fly randomly with velocity v_i at position x_i with a fixed frequency f_min (or wavelength λ), varying wavelength λ (or frequency f) and loudness A₀ to search for prey. They can automatically adjust the wavelength (or frequency) of their emitted pulses and adjust the rate of pulse emission rÌ[0,1], depending on the proximity of their targets;

· Although the loudness can vary in many ways, we assume that the loudness varies from a large (positive) A₀ to a minimum value A_min.

Another obvious simplification is that no ray tracing is used in estimating the time delay and three dimensional topographies. In addition to these simplified assumptions, the following approximations have been used, for simplicity. In general the frequency f in a range [f_min, f_max] corresponds to a range of wavelengths [λ_min, λ_max]. For example, a frequency range of [20 kHz, 500 kHz] corresponds to a range of wavelengths from 0.7 mm to 17 mm.

In simulations, we use virtual bats naturally. We have to define the rules how their positions x_i and velocities v_i in a d-dimensional search space are updated. The new solutions x_i⁰  and velocities v_i⁰ at time step t are given by:

	(6)
	(7)

where βÌ[0,1] is a random vector drawn from a uniform distribution. Here x₀ is the current global best location (solution) which is located after comparing all the solutions among all the n bats. As the product λ_if_i is the velocity increment, we can use either f_i (or λ_i) to adjust the velocity change while fixing the other factor λ_i (or f_i), depending on the type of the problem of interest. For the local search part, once a solution is selected among the current best solutions, a new solution for each bat is generated locally using random walk:

(8)

where EÌ[0,1] is a random number, while = A^t = < A^t_j > is the average loudness of all the bats at this time step.

Based on the above approximations and idealization, the pseudo-code of the Bat Algorithm (BA) can be summarized below.

The loudness usually decreases once a bat found its prey and rate of pulse emission increases. In our experiments, the loudness and pulse emission rate are varied once a solution is improved. The bat is moving towards optimal solution according to:

(9)

where α and γ are constants [7]. Figure 1 represents flowchart of the Bat Algorithm.

Results and Discussion

This paper presents the development of Bat Algorithm for solving an economic dispatch problem with six units. The programs are written in MATLAB software package.

The generator cost coefficients; generation limits and B-coefficient matrix of six unit system are given below. Economic Load Dispatch solution for six unit system is solved using BAT algorithm.

The cost coefficients and power limits of our 6 unit system are given in Table1.

Table 1.Cost coefficients and power limits of 6 unit system.

Unit	an	bn	cn	Pn,min	Pn,max
1	756.79886	38.53	0.15240	10	125
2	451.32513	46.15916	0.10587	10	150
3	1049.9977	40.39655	0.02803	35	225
4	1243.5311	38.30553	0.03546	35	210
5	1658.5696	36.32782	0.02111	130	325
6	1356.6592	38.27041	0.01799	125	315

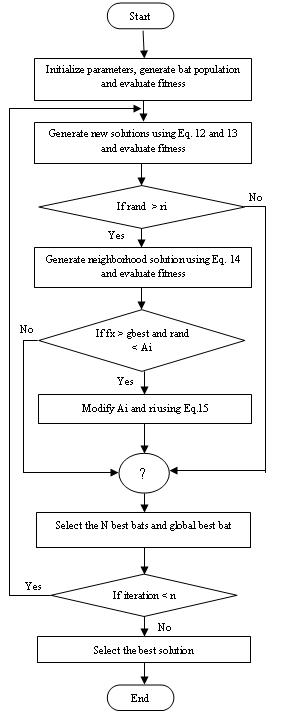
Figure 1. Flowchart of the Bat Algorithm

The loss co-efficient matrix of 6-Unit system:

(9)

Table 2 shows the powers generated with the method of bat algorithm by varying demand.

Table 2.Test results of BAT algorithm for 6-Unit System: Power dispatch (MW)

Power demand (MW)	BA
	P1	P2	P3	P4	P5	P6
600	23.8587	10.0000	95.6376	100.7030	202.8428	181.1953
650	26.0690	10.0000	107.2678	109.6703	216.7651	196.9558
700	28.2911	10.0000	118.9568	118.6753	230.7668	212.7419
750	30.4787	11.2272	130.4517	127.5111	244.4575	228.1844
800	32.5877	14.4827	141.5491	136.0426	257.6603	243.0085
850	34.7084	17.7685	152.7123	144.6200	270.8849	257.8618
900	36.8470	21.0780	163.9343	153.2216	284.1710	272.7362
950	39.0000	24.4149	175.2179	161.8868	297.4793	287.6303

In table 2 is seen that the results obtained by the method of Bat algorithm are satisfactory.

To verify the effectiveness of our method (BA), we fixed power demand at 700MW and the results obtained by bat algorithm are compared with other methods such as Genetic Algorithm (GA) [8], PSO [9] and Simulated Annealing (SA) [10], and the results of this comparison are shown in Table 3.

Table 3.Comparison results between BA, GA, PSO and SA

	AG[8]	PSO[9]	SA[10]	BA
P1	21.4220	29.2400	28.2942	28.2911
P2	23.6700	12.5700	10.0001	10.0000
P3	118.0564	118.9667	118.9561	118.9568
P4	118.3270	118.3270	118.6795	118.6753
P5	230.5502	230.7553	230.7623	230.7668
P6	230.7945	212.7338	212.7395	212.7419

The results of comparison of table 3 are represented by the graph of the Figure 2.

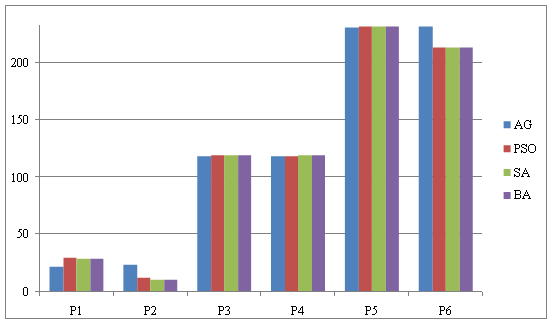
Figure 2. Graph showing the result of comparison between BA, GA, PSO and SA

The result of comparison between BA, GA, PSO and SA obtained from Table 2 shows that the method bat algorithm gives better results.

Additionally, the advantages of BAT algorithm are that BAT algorithm is easier to implement and there are fewer parameters to adjust.

Conclusions

The results obtained by applying the proposed algorithm were compared to those obtained by AG, PSO and SA. The BAT algorithm has superior features, including quality of solution, stable convergence characteristics and good computational efficiency. The comparison shows that BAT algorithm performs better than the mentioned methods.

Therefore, BAT optimization is a promising technique for solving complicated problems in power system.

References

1. Mahor A., Prasad V., Rangnekar S., Economic Dispatch Using Particul Swarm Optimization: a Review, Renewable and Sustainable Energy Reviews, 2009, 13, p. 2134-2141.

2. Application of the firefly Algorithm for Solving the Economic Emission Load Dispatch Problem, International Journal of Combinatorics, 2011, 2011, 23, p.1.

3. Bandi R., Chandra J., Mohan V., V. Reddy V.C., Application of Bat Algorithm for Combined Economic Load and Emission Dispatch, International Journal of Electrical and Electronic Engineering & Telecommunications, 2013, 2(1), p. 1-9.

4. Sudhakara K., Damodar M., Economic Load Dispatch Using Firefly Algorithm, International Journal of Engineering Research and Applications, 2012, 2, p. 2325-2330.

5. Yang X.S., Engineering Optimization an Introduction with Metaheuristic Applications, New Jersey, Published by John Wiley & Sons, 2010.

6. Yang X.S. Nature-Inspired Metaheuristic Algorithms, United Kingdom, Second Edition Published by Luniver Press Frome, 2010.

7. Gherbi F.Z., Lakdja F., Environmentally Constrained Economic Dispatch via Quadratic Programming, International Conference on Communication, Computing and Control applications, (ICCCA’11), at Hammamat, 2011, Tunisia.

8. Adhinarayanan T., Sydulu M., Directional Search Genetic Algorithm Application to Economic Dispatch of Thermal Units, International Journal of Computational Methods in Engineering Science and Mechanic, 2008, 2, p. 211-216.

9. Slimani L., Contribution à L’application de L’optimisation par des Méthodes Métaheuristiques à L’écoulement de Puissance Optimal dans un Environnement de L’électricité Dérégulé, Doctorate thesis of electrical engineering, Batna university, Algeria, 2009.

10. Yahiaoui F.Z., Ait ouali D., contribution à l’étude du dispatching economic en utilisant la méthode de recuit simulé (Simulated Annealing), Master thesis, Sidi Bel Abbes University, Algeria, 2012.

11. Gherbi Y.A., Bouzeboudja H., Lakdja F., Application of Firefly and Bat Optimization Algorithms to Economic Dispatch, Troisième Conférence Internationale sur la Maintenance, la Gestion, la Logistique et l’Electrotechnique (CIMGLE’2013), Paris – France, 13-15 Novembre 2013.

12. Gherbi Y.A., Bouzeboudja H., Lakdja F., Gherbi F.Z., Ould-Abdeslam D., Environmentally constrained economic dispatch via bat algorithm, International Conference on Electrical Engineering and Automatic Control (ICEEAC 2013), Setif, Algeria, 24-26 November 2013.