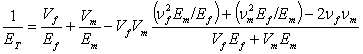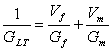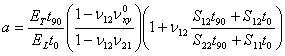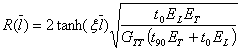Evaluation of the stiffness of composite materials with hygrothermal conditions
Khaled AMARA1*, Mokhtar BOUAZZA2, Kamel ANTAR3 and Abdelkader MEGUENI3
1 Department of Civil Engineering, University centre of Ain Témouchent, 46000, Algeria
2 Department of Civil Engineering, University of Bechar, Bechar 08000, Algeria.
3 Laboratory of Materials and Hydrology (LMH), University of Sidi Bel Abbes, 2200, Algeria.
E-mails: amara3176@yahoo.fr; bouazza_mokhtar@yahoo.fr; mech2003@hotmail.com
* Corresponding author, Phone: +213663248283
Abstract
The change in longitudinal modulus as a result of transverse ply cracking in simple cross-ply laminate is examined theoretically with the taking into consideration the decrease of the mechanical properties of material by the variation of temperature and moisture. The results show that the hygrothermal environment has a significant effect on the relative reduction of longitudinal Young’s modulus at the higher crack density, in contrast with the complete reduction of longitudinal Young’s modulus in which the sensitivity of the hygrothermal effects become weaker but significant at the lower crack density.
Keywords
Hygrothermal effect; Stiffness; Cross-Ply laminate; Crack density
Introduction
The variation of temperature and moisture reduces the elastic moduli and degrades the strength of the laminated material [1–8].
Also the environmental conditions in terms of temperature and moisture induce the hygrothermal stresses within the plies [9–13]. Furthermore, hygrothermal aging in the absence of external loads can lead to spontaneous formation of matrix micro cracks in laminates [14].
On the other hand, when cross-ply laminates are subjected to tensile loading, the first observed damage modes in cross-ply laminates is matrix cracking which cause the reduction of longitudinal Young’s modulus of laminates. These cracks are in general not critical for final failure. In order to design structure properly it is necessary to understand the damage process and to predict the level of degradation of mechanical properties as a result of transverse ply cracking in cross-ply laminate when this latter is exposed to hygrothermal ageing before applying the mechanical loading.
In the present study, the hygrothermal stresses [8-11] and the water-induced micro cracks [12] are not taken into consideration. But the material properties are assumed to be functions of temperature and moisture. Both ambient temperature and moisture are assumed to have a uniform distribution. The plate is fully saturated such that the variation of temperature and moisture are independent of time and position.
The changes of longitudinal Young’s modulus of laminate due to the number of cracks formed in transverse layer are determined here, using two approaches: shear lag model [15–17] and Hashin’s model [18].
These latter, are modified to take into account the changes of the elastic moduli which are related to environmental conditions.
Material and method
It is well known in many studies [3-6] that the material Properties are function of temperature and moisture. In terms of a micro-mechanical model of laminate, the material properties may be written as [7-10]
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
In the above equations ![]() and
and ![]() are the fiber and matrix volume fractions and are related
by:
are the fiber and matrix volume fractions and are related
by:
|
|
(5) |
And Ef, Gf, and vf are Young's modulus, shear modulus and Poisson's ratio of fibers, respectively, Em, Gm and vm are the properties corresponding to the matrix.
EL, ET, GLT are the longitudinal modulus, transversal modulus and shear modulus, respectively.
It is proved that the longitudinal modulus Em of matrix is a function of temperature and humidity, therefore, EL, GLT and ET are also a function of temperature and humidity. The longitudinal modulus of the damaged cross-laminated in the x direction is given by [19]:
|
|
(6) |
where: Ex, Ex0 are respectively the longitudinal modulus after damage and before damage.
![]() ,
, ![]() and α is a known function,
dependent on elastic properties and geometry of 0° and 90° layer:
and α is a known function,
dependent on elastic properties and geometry of 0° and 90° layer:
|
|
(7) |
where R(l) is the stress perturbation function
|
|
(8) |
GTT out of plane shear modulus, t90 half thickness of the 90° layer and t0 thickness of the 0° layer
The properties of composite laminates studied AS4/3502 are given in the following Table1
Table 1: The properties of the composite laminate.
|
Material |
EL (GPa) |
GLT (GPa) |
ET (GPa) |
GTT (GPa) |
|
|
h0 (mm) |
|
AS4/3502 [12] |
144.8 |
9.58 |
4.79 |
4.2 |
0.31 |
0.4 |
0.147 |
Results and discussion
Comparison of predictions with experimental data
Figure 1 and Figure 2 also show the phenomenon of reduction of the stiffness that is aggravated by the increased thickness of the layer 90°, i.e. the reduction of stiffness becomes larger when the thickness of the layer 90 augment, he is able to understand that increasing the thickness of the layer of 0° has a strong constraint on transverse cracking in the layer at 90° because the more the load is carried by the 0°.
Hygrothermal effect on the reduced elastic properties
The study, here, has been focused on the stiffness reduction due to transverse ply cracking in simple hygrothermal aged angle-ply laminate [0n/90m] S.
For that, several numerical examples were presented. Graphite/epoxy composite material was selected in the present examples.
However, the analysis is equally applicable to other types of composite material.
For these examples the thickness of each ply is 0.125 mm and the material properties adopted are: Ef = 230 GPa, Gf = 9GPa, vf = 0.203, vm = 0.34 and Em = (3.51-0.003T-0.142 C) GPa, in which T = T0 + ΔT and T0 = 25°C (room temperature), and C = C0+ΔC, C0 = 0wt. % H2O.
Three sets of environmental conditions are considered, referred to as 1, 2 and 3.
For environmental case 1, T=25°C, so that both ΔT and ΔC are zero.
For environmental case 2, ΔT=50°C and ΔC=0.5%, and for environmental case 3, ΔT=100°C and ΔC=1%. The environmental of case 1 will be regarded as the reference case. We calculate here, the loss of stiffness in the damaged laminate, which is already subjected to the hygrothermal ageing of type 1, 2 or 3.
The loss of stiffness in the laminate as a result of crack density is evaluated compared to the initial stiffness of the uncracked laminate.
We note that this initial stiffness of the uncracked laminate is function of temperature and moisture. Consequently, Eq. (6) becomes:
|
|
(9) |
The index (i) represents the considered case of the environmental conditions (case 1, 2 or 3).
Figures 3 and 4 illustrate the variation of the reduction of the longitudinal Young's modulus for various types of environmental conditions considered. The modulus reduction depends in addition to the crack density on the moisture and temperature. In fact, the longitudinal Young’s modulus is reduced with decreases in moisture and temperature especially when the crack density becomes higher.

Figure 1. Stiffness reduction with different crack densities for [0/90] s and [02/902] s AS4/3502 laminate

Figure 2. Stiffness reduction with different crack densities for [0/902]s and [0/903]s AS4/3502 laminate

Figure 3. Hygrothermal effect on the longitudinal Young’s modulus degradation for [0/902] s AS4/3502 laminate
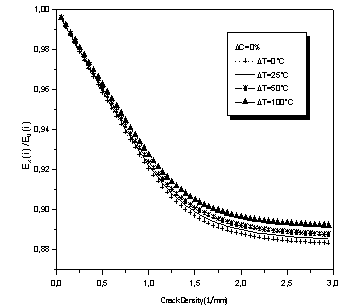
Figure 4. Stiffness reduction with different crack densitiesfor [0/902]s AS4/3502 laminate under different temperature
Conclusions
The material properties were considered to be dependent on temperature and moisture, which are given explicitly in terms of the fibre and matrix properties and the fibre-volume ratio.
The results show that the longitudinal Young’s modulus degradation due to the transverse cracking is also reduced with decreasing moisture concentration and temperature, especially when the crack density takes higher values. However, this reduction is not very important.
In order to assess the effects of temperature and moisture on the reduction of longitudinal Young’s modulus in cross-ply laminates containing transverse cracking. The material properties are considered to be dependent on temperature and moisture, which are given explicitly in terms of the fiber and matrix properties and fiber volume ratio. The solution methodology is general in nature and may be applicable to the analysis of other types of environmental conditions, e.g. including the hygrothermal coupling in the governing equations.
The results presented herein show that the relative longitudinal Young’s modulus is reduced with decreases in moisture and temperature especially when the crack density becomes higher.
References
1. Shen C.H., Environmental effects in the elastic moduli of composite material, Environmental effects on composite materials, Technomic Publishing Company, Inc., Westport, CT, 1981, p. 94-108.
2. Adams D.F., Miller A.K., Hygrothermal micro stresses in a unidirectional composite exhibiting inelastic materials behaviour, Journal of Composite Materials, 1977, 11, p. 285-299.
3. Bowles D.E., Tompkins S.S., Prediction of coefficients of thermal expansion for unidirectional composites, Journal of Composite Materials, 1989, 23, p. 370-381.
4. Upadhyay P.C., Lyons J.S., Effect of hygrothermal environment on the bending of PMC laminates under large deflection, Journal of Reinforced Plastics and Composites, 2000, 19(6), p. 465-491.
5. Shen H.S., The effects of hygrothermal conditions on the post buckling of shear deformable laminated cylindrical shells, International Journal of Solids and Structures, 2001, 38, p. 6357-6380.
6. Shen H.S., Hygrothermal effects on the post buckling of shear deformable laminated plates, International Journal of Mechanical Sciences, 2001, 43, p. 1259-1281.
7. Shen H.S., Hygrothermal effects on the post buckling of axially loaded shear deformable laminated cylindrical panels, Composite Structures, 2002, 56 (1), p. 73-85.
8. Tounsi A., Adda-Bedia E.A., Simplified method for prediction of transient hygroscopic stresses in polymer matrix composites with symmetric environmental conditions, International Journal of Applied Composite Materials, 2003, 10(1), p. 1-18.
9. Benkeddad A., Grediac M., Vautrin A., Computation of transient hygroscopic stresses in laminated composite plates, Composites Science and Technology, 1996, 56, p. 869-876.
10. Benkeddad A., Grediac M., Vautrin A., On the transient hygroscopic stresses in laminated composite plates, Composite Structures, 1995, 30(2), p. 201-205.
11. Hahn H.T., Kim R.Y., Swelling of composite laminates, Advanced Composite Materials Environmental Effects, ASTM STP, 1978, 658, p. 98-120.
12. Kim H.W., Grayson M.A., Nairn J.A., The effects of hygrothermal aging on the microcracking properties of some carbon fiber/polyimide laminates, Advanced Composite Letters, 1995, 4, p. 185-188.
13. Highsmith A.L., Reifsnider K.L., Stiffness reduction mechanisms in composite laminates, Damage in Composite Materials, 1982, ASTM STP, 775, p. 103-117.
14. Han Y.M., Hahn H.T., Ply cracking and property degradation of symmetric balanced laminates under general in plane loading, Composites Science and Technology, 1989, 35, p. 377-397.
15. Lim S.G., Hong C.S., Prediction of transverse cracking and stiffness reduction in cross-ply laminated composites, Journal of Composite Materials, 1989, 23, p. 695-713.
16. Elmeiche, A. T., Adda-Bedia E., Megueni A., Analysis of the transverse cracking in hybrid cross-ply composite laminates, International Journal of Computational Materials, Science, 2009, 46, p. 1102-1108.
17. Fellah M., Tounsi A., Amara K.H., Adda Bedia E.A., Effect of transverse cracks on the effective thermal expansion coefficient of aged angle-ply composites laminates, Theoretical and Applied Fracture Mechanics, 2007, 48, p. 32-40.
18. Hashin Z., Analysis of cracked laminates: A variational approach, Journal of Mechanics Materials, 1985, 4, p. 121-136.
19. Joffe R., Varna J., Analytical modelling of stiffness reduction in symmetric and balanced laminates due to cracks in 90°-layers, Composites Science and Technology, 1999, 59, p. 1641-1652.