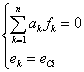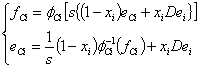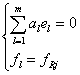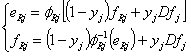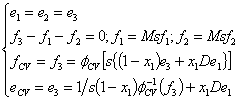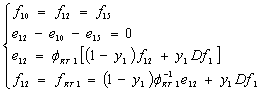Optimal sensors placement for monitoring a steam condenser of the distillation column using bond graph approach

Samia LATRECHE^*, Mohammed MOSTEFAI, Mabrouk KHEMLICHE

Automatic Laboratory of Setif, Electrical Engineering Department, University of Setif 1, 19000, Setif, Algeria

E-mails: ksamia2002@yahoo.fr, mostefai@univ-setif.dz, mabroukkhemliche@yahoo.fr

^* Corresponding author, Phone: +213668769714; Fax: +213 36 92 51 02

Abstract

This paper deals with monitoring of a process engineering system. The steam condenser was monitored by bond graph tool. The model was constituted by nine capacitive and resistive elements which needed minimum of sensors. This method was based on Analytical Redundancy Relations which were generated from a condenser model and represented residuals. After substitution, we obtained the placement of six sensors which guaranteed the monitoring of nine components. A fault is created by the abrupt annulment of the fluid flow value provided by the source. The block diagram is elaborated on SYMBOLS software and we supervised the residuals evolution.

Keywords

Optimization; Sensors placement; Monitoring; Condenser; Distillation Column; Bond graph

Introduction

The monitoring system with rigid structure knows progress during the last years. The monitoring of the thermal system is difficult because of the phenomenon complexity [1]. These industrial processes have a strongly nonlinear behaviour due mainly to the mutual interaction of several phenomena with various nature and the association of the technological components. The system modelled and monitored, is a condenser of the distillation column which is produced thermal, chemical and hydraulic phenomena. In this case, the bond graph tool reduces all difficulties because of its causal and structural properties. After the validation of the model, the placement of the sensors, is made and followed by the research of the optimal case [2], and [3]. The advantages of applying bond graph model to the condenser of distillation column are the ability to build a graphical circuit, the use of detailed equations, the encapsulation of pieces of the model into sub-models and the representation of the system power flows in details. The main drawback of using bond graphs is that they cannot describe distillation equations. In this work, both bond graph modelling and monitoring by sensors placement are proposed for a condenser of a distillation column.

Description of the system

The condenser schematic is shown in Figure 1. The steam enters at the left side, condensed on the pipes filled with cooling water.

It falls to the floors and leaves from there to the receiver through control valves [1]. The water outflow (condensate) is controlled by three valves in order to keep its level constant. The condenser is a module of four input-outputs. It is composed by a coolant circuit made up of a unit of pipes which lead the liquid. The liquid phase of cold fluid accumulates heat while passing in steam (vapor) phase. When the steam flow attempts the condenser, a contact is obtained between the steam and the pipes of the fluid circuit in which circulate both the cold fluid and the steam condensed in fine droplets which are formed at the condenser bottom [4].

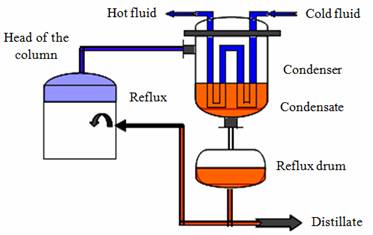
Figure 1. The condenser operating in the distillation column

Steam circulating in the column is from a portion of the feed when it is vaporized. In the boiler, the liquid mixture of the beginning is heated for the vaporizer. The steam which arrives in the line of column heading is condensed completely or partially by a condenser [5], [6]. When the steam arrives in contact with the fluid pipes in which circulates a cold fluid, it was condensed in liquid which runs out downwards by simple gravity and collected at the bottom of the condenser. The liquid obtained is generally returned in the column under the name of backward flow by tubular of feed. The other part is collected like a distillate and the non-vaporized part comes to contribute to the liquid flow. The operation is repeated, by ensuring the condensation of the steam of column heading [2].

Sensors placement algorithm

This procedure consists of an optimal sensors placement for the components monitoring, i.e. to detect and to isolate the components failures. From a physical process we elaborate a bond graph model. In bond graph model, sensors are placed only at the junction 0 and 1, we consider a virtual placement of the sensor at the position j, which is represented by the variables x and y. N₀, and N₁ are respectively the junction numbers 0_Ci, 1_Rj. i, j, n and m are respectively the junction orders, the number of the bonds’ fixed on the junction 0_Ci, 1_Rj. The structural equations of the junction s0_Ci, which describe the effort equality and the pressure conservation produced in C element, are given by (1).

(1)

where f_k and e_k are respectively the flow and the effort of the junction number k; a_k=+1 if the bond graph semi flow is toward junction; a_k=-1 otherwise. For the nonlinear functions Ф_Ci and s the Laplace coefficient used here as the derived operator, the flow and the effort variables are determined by (2) as follows:

(2)

where i=1, N₀ ; De_i effort detectors, x_i binary variables x_i=1 if we place detector; x_i=0 otherwise. The structural equations of the junctions 1_Rj are given by equation (3).

(3)

For the nonlinear functions Ф_Rj, the flow and effort variables are determined by (4):

(4)

where j=1, N₁; Df_j flow detectors, y_j binary variables y_j =1 if we place detector; y_j =0 otherwise. The combinations of the variables x_i and y_j make it possible to generate analytical redundancy relations which give the structures of the residuals. The bond graph model of the condenser in the distillation column representing hydraulic and thermal phenomena with steam and liquid phases and using sensors placement (effort and flow detectors) is represented by Figure 2. This model is composed by 5 junctions type 0 attached to 5 components C_V, C_L, C_T1, C_T3 and C_TS noted 0₁, 0_2, 0_3, 0_4, 0₅  and 4 junctions type 1 attached to 4 components R_T1, R_T3, R_TS and R noted 1₁, 1₂, 1₃, 1₄ [2]. These components are: C_V the pipe capacity traveled by fluid in vapor phase, C_L the pipe capacity of fluid in liquid phase; C_T1 the tank₁ capacity; C_T3 the tank₃ capacity; C_TS the tank capacity of a distillate; R_T1, R_T3, R_TS and R are respectively, the valves of tank₁ and tank₃, the distillate and the reflux drum.

Table 1. Nomenclature

Variables	Bond graph descriptions	Physical descriptions
E	Effort	Pressure P, Temperature T
F	Flow	Masse flow dm/dt, Enthalpy flow dH/dt
De	Effort detector	Measured effort
Df	Flow detector	Measured flow
Se, MSe	Effort source	Thermal or Hydraulic effort
Sf, MSf	Flow source	Thermal or Hydraulic flow
R	Resistive component	Valve
C	Capacitive component	Tank
ARR	Analytical Redundancy Relation	Residual (Failure indicators)
S	Derivative operator	d/dt
1/s	Integral operator	∫dt
Φ	Nonlinear components evolution	ΦR; ΦCV; ΦCL; ΦCT1; ΦCT3; ΦCTS; ΦRT1; ΦRT3; ΦRTS
CV	Vapour (steam) capacity	Pipe capacity travelled by fluid in vapour phase
CL	Liquid capacity	Pipe capacity travelled by fluid in liquid phase
CT1	Tank1 capacity	Level of fluid into tank1
CT3	Tank3 capacity	Level of fluid into tank3
CTS	Capacity of distillate tank	Distillate into reflux drum
RT1	Tank1 resistor	Valve of fluid into tank1
RT3	Tank3 resistor	Valve of fluid into tank3
RTS	Resistor of distillate tank	Distillate valve

The bond graph model is described as follows:

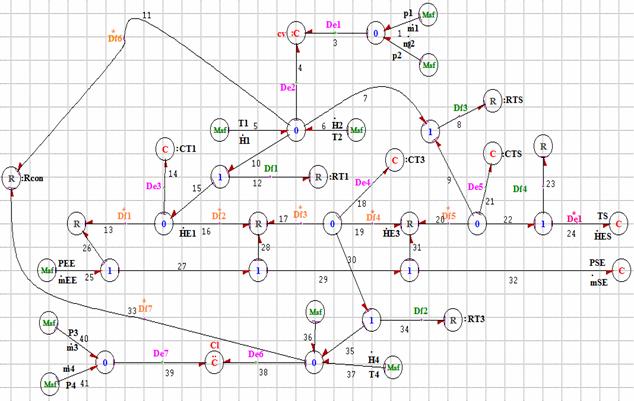
Figure 2. Bond graph model of the condenser with sensors placement

Constitutive and structural equations

The calculation of the residuals needs application of the previous algorithm by generating flow f and effort e of all junctions. For example, the junctions 0_De1 and 1_Df1 are described by the equations (5) and (6).

	(5)
	(6)

where Msf₁ and Msf₂ represent the controlled (modulated by signals) flow source of bond 1 and bond 2. From the previous equations we can deduce the system (7) which permits us to generate residuals:

(7)

Optimization technique

The equations above allow according to binary variables x_i and y_j determining the final system structure to supervise. The optimal case is with how many sensors to supervise this model. There exist 2ⁿ = 2⁹ = 512 combinations to obtain the optimal case.

From the combination with 9 sensors placed in the 9 positions, the ARRs are calculated until to obtain the optimal combination. The detection is defined by columns of the signature table different to zero. The isolation is guaranteed by the columns different each other.

In the second step, the substitution is used to reduce the number of ARRs and to verify the monitoring from the signature table. In our case, 6 ARRs satisfied that all the components are monitored. The generated ARRs are given by the following relations (the sensors are placed only if x_i and y_j = 1).

Substitution with 9 sensors

All the sensors are placed, so each component is monitored by one sensor and the system (7) becomes as follows for [x₁ y₁ x₂ y₂ x₃ y₃ x₄ y₄ x₅ x₆ x₇]^T = [11011111110]^T

(8)

Table 2. Faults signature table for 9 detectors

	CV	CL	CT1	RT1	CT3	RT3	CTS	RTS	R
ARR1	1
ARR2	1			1
ARR3						1
ARR4			1
ARR5	1							1
ARR6					1
ARR7									1
ARR8							1
ARR9	1

In this case faults on all the components are detectable and localizable.

Substitution with 8 sensors

One of the possible combinations is chosen, so 8 ARRs are generated for monitoring 9 components. The combination used in the system (7) is [01101111110]^T.

(9)

Table 3. Faults signature table for 8 detectors

	CV	CL	CT1	RT1	CT3	RT3	CTS	RTS	R
ARR1				1
ARR2	1
ARR3			1
ARR4								1
ARR5					1	1
ARR6									1
ARR7							1
ARR8		1				1

In this case faults on all the components are detectable and isolable.

Substitution with 7 sensors

Not localizable case [01000111111]^T

(10)

Table 4. Faults signature table for 7 detectors

	CV	CL	CT1	RT1	CT3	RT3	CTS	RTS	R
ARR1	1		1	1
ARR2					1	1
ARR3									1
ARR4							1
ARR5							1
ARR6		1
ARR7	1							1

The fault on (C_T1 and R_T1) and the fault on (C_T3 and R_T3) are not localizable (the same column vectors).

Detectable and isolable case [00101111110]^T

(11)

Table 5. Faults signature table for 7 detectors

	CV	CL	CT1	RT1	CT3	RT3	CTS	RTS	R
ARR1	1			1
ARR2			1
ARR3								1
ARR4					1	1
ARR5									1
ARR6							1
ARR7		1				1

Substitution with 6 sensors [01001111010]^T

(12)

Table 6. Faults signature table for 6 detectors

	CV	CL	CT1	RT1	CT3	RT3	CTS	RTS	R
ARR1	1			1
ARR2			1
ARR3	1						1	1
ARR4					1	1
ARR5							1		1
ARR6		1				1

All the combinations with 5 sensors placed cannot ensure the detection and the isolation of the failures that affect this system. The optimal case is to monitor 9 components by only 6 sensors.

The table (6) of the residuals structure permit to notice that the residuals structures are different and the faults signatures are different and not equal to zero, thus the components C_V, C_L, C_T1, R_T1, C_T3, R_T3, C_TS, R_TS and R are monitored.

Sensitivity of the detectors

Under normal operating, the residuals must be constantly equal to zero but it is not always the case because of the modelling errors and the unavailability of the technical specifications of the real system.

From SYMBOLS software (System Modelling Bond graph Language Simulation), we have implanted the bond graph model [5] associated to the block diagram of the ARR that contain affected components.

We create fault on R_T1 component monitored by the detector Df₁ (disturbance from the association of Dirac pulse and Unit echelon). Their values are not considered only their appearances in the relation are taking into account with evaluation term (1 for the presence and 0 for the absence).

In the first time, the fault is created between the instant t₁=2s and t₂=2.01s by the annulment of fluid flow provided by the source [9], [10].  

In the second time, the block diagram of the ARR₁, ARR₂ and ARR₃ expressions that contain Df₁ detector (see Figure. 3) is elaborated. The three outputs are represented by three scopes.

The failure is injected on 1_RT1 junction monitored by the detector Df₁ (Figure. 4) and not sensitive to ARR₄, ARR₅ and ARR₆ (Figure. 5). It represents sealing in the valve and leakage in the tank.

Figure 3. Block diagram representing the ARRs function of Df₁

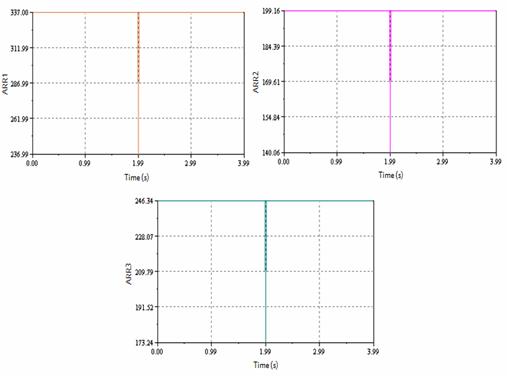
Figure 4. Sensitivity of Df₁ detector with failed operating of ARR₁, ARR₂ and ARR₃

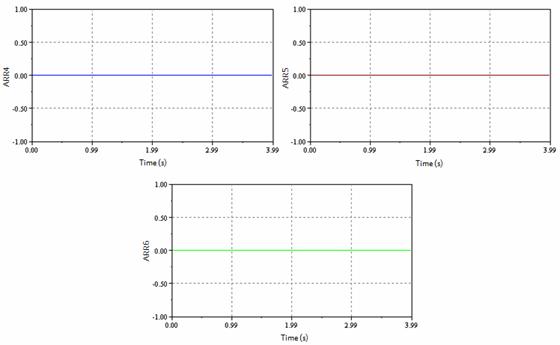
Figure 5. Sensitivity of Df₁ detector with normal operating of ARR₄, ARR₅ and ARR₆

The residuals ARR₁, ARR₂ and ARR₃ are sensitive to the failures, it is due to the fact that the Df₁ detector appears strongly in these residuals, on the other hand residuals ARR₄, ARR₅ and ARR₆ are null because the detector does not appear in the relations of these residuals it is the normal operating.

Conclusions

The bond graph tool used for modelling and monitoring is very efficient because of the complexity of the phenomena that are produced in the steam condenser as hydraulic and thermal phenomena and the separation between steam and liquid phases.

The Analytical Redundancy Relations are deduced from graphical model of the steam condenser of the distillation column.

The structural junction equations and constitutive element laws for generating these relations are used as the failures indicators.

The algorithm used for researching the optimal case is very efficient.

The simulator of Symbols Software allows the validation and simulation of the model. The technique applied to steam condenser for components monitoring can be extended to detect and locate failures actuators and sensors.

Acknowledgements

Corresponding author would like to thank Prof. Mohammed Mostefai my PhD supervisor and Prof. Mabrouk Khemliche the Head of Automatic Laboratory of Setif –Algeria for performing the present work.

References

1. Raudensky M., Hnizdil M., Hwang J. Y., Lee S. H., Kim S. Y., Influence of the water temperature on the cooling intensity of mist nozzles in continuous casting, Journal of materiali in tehnologije / Materials and Technology, 2012, 3, p. 311-315.

2. Latreche S., Khemliche M., Mostefai M., Modeling and simulation of the distillation column boiler, Asian Journal on Information Technology, 2006, 5(8), p. 823-828.

3. Nan T., Jinjia W., Jiabin F., Experimental and numerical study on the thermal performance of a water/steam cavity receiver, Energies Journal, 2013, 6(3), p. 1198-1216.

4. Ould Bouamama B., Thoma J. U., Cassar J.P., Bond graph modeling of steam condensers, In: IEEE International conference on systems, man, and cybernetic Orlando (USA), 1997, p. 490-494.

5. Cicile J.C., Distillation, Absorption, Généralités sur les colonnes de fractionnement, Technique de l’Ingénieur, Traité de Génie des Procédés, J 2 621, 1999.

6. Thoma J.U., Ould Bouamama B, Modelling and simulation in thermal and chemical engineering. Bond graph approach, Springer - Verlag, Berlin, Germany, 2000.

7. Medjaher K., Samantary A. K., Ould Bouamama B, Bond graph model of a vertical U-tube steam condenser coupled with a heat exchanger, International Journal of Simulation Modelling Practice and Theory, 2009, 17(1), p. 228-239.

8. Khemliche M., Ould Bouamama B., Haffaf H, Sensors placement for diagnosability on bond graph model, Sensors and Actuators Journal, Elsevier  A-physical, 2006, 4, p. 92-98.

9. Kozak D., Ivandic Z., Kontajic, P, Determination of the critical pressure for a hot-water pipe with a corrosion defect, Materiali in tehnologije / Materials and Technology, 2010, 6, p. 385-390.

10. Badoud A., Khemliche M., Latreche S, Modeling, simulation and monitoring of nuclear reactor using directed graph and bond graph, Proceedings of World Academy of Science, Engineering and Technology, 2009, 37, p. 199-208.