A study on fractality properties of nano particles scanning electron microscopy images
Shahrbano MALEKI, Shahriar GHAMMAMY and Jaber SALEHZADEH*
Department
of Chemistry, Faculty of Science, Islamic
E-mail: chem.salehzadeh@yahoo.com
* Corresponding author, Phone: +98 9144524649; Fax: +98 4512239088
Abstract
Measuring fractal dimensions has become a common practice for describing structural properties of porous media. The present paper studies computing method of fractal dimension by using the image storing principles on computer. As an example of its application on nano particles surface structure, by applying Matlab, the binary image and matrix about the surface pore were investigated by processing and analyzing the Scanning Electron Microscopy (SEM) images of nanoparticles. In accordance with the nanoparticles characteristics of binary digital images, have been minutely discussed based on the fractal theory that the principle and method of calculating Fractal dimensions (D) by use of box-counting dimension.
Keywords
Scanning electron microscopy; Binary image; Box-counting dimension; Fractal dimension
Introduction
Fractal geometry is an excellent mathematical approach in the study of irregular geometric objects. Fractal dimension can indicate some nanoparticles characteristics of images obtained from nature. The application of fractal theory allows description of various states of fragmenting and branching in biological, ecological and other systems [1-6].
Because processing the image is in the divided windows using Matlab to compute fractal dimension (D), the whole result of counting the boxes and every pixel of fractal image can be observed. At the same time, because of its powerful function in displaying figure, Matlab can display the binary image with fractal nanoparticles characteristic.
The fractal property is a physical property expressed at the super molecular level, at a microscopic scale and at a macroscopic scale. Fractal geometry has been used to nanoparticles characterize the surface structure, nanoparticles characteristic and irregularities of solid materials. Fractal dimensions are numbers used to quantify these properties. Fractal geometry has emerged recently as an analytical tool which is suitable for the description of complex structures, such as those which are found in most porous objects [7]. It has been used to embellish the morphology of highly irregular objects imbedded onto two and three dimensional space and is defined as two and three-dimensional fractal dimensions [8].
This paper proposes a quantitative method to analyze the nanoparticles from SEM images using image processing and statistical analysis in Matlab, a pixel-covering method to cover the object being analyzed with grids having the same dimensionality as the containing space.
Material and method
Images analysis
The four images [9-11], that Matlab processes were digital images, which are actually quantified into two-dimension sampling array. The gray variation of SEM images could represent the roughness and distribution of nanoparticles surface pore, so the SEM images need to be processed in order to convert it into black-white images whose gray value is between 0-255 by software Photoshop.
Obtaining binary images and matrix
In Figure 1 the area that has been marked with 1 is just a cluster in Matlab analysis, and the size and number of the area shows the dimension and quantity of the cluster.
After images segmentation, conversing SEM images to binary images, each pixel in the new one is either black or white. Then, through the Matlab program the binary images were converted to a data file, which was in the form of a matrix. All the elements of the matrix correspond to the pixels of the binary images, and the element value is either 1 (white) or 0 (black), which is determined by the color of the pixel in the binary images. For the matrix, the mathematical computation software Matlab, which has a variety of toolboxes including images processing, was used in computations.

Figure 1. Binary images as they have been used for the measurements of the fractal dimension
Measurement of fractal dimensions
We used the box counting method to measure fractal dimensions, or more specifically, fractal capacity dimensions of the pore and the matrix phase. These dimensions can be described by the ratio between the logarithm of an iteration rule and the logarithm of the scale increment [12].
There are several different concepts of the fractal dimension of a geometrical configuration. The most famous method of calculating fractal dimensions in the natural sciences is the so called box counting dimension [13, 14]. A basic principle to estimate fractal dimension is based on the concept of self-similarity. The property of self-similarity implies that the form of an object is invariant constructed of an infinite number of copies of itself. The fractal dimension D of a bounded set A in Euclidean n-space, using box counting of a set A in a grey image is given by [15]:
|
|
(1) |
where Nr denotes the number of boxes of side length r = 2n, n = 1, 2, 3, 4 (number of distinct copies of A in the scale). The box-counting method is the most desirable method for image fractal dimension estimation because it can apply fractal patterns with or without self-similarity.
Thus, whenever measured box counts can be described by Eq. (1) using a non-integer value for D, the feature is considered to be a fractal with D as the fractal dimension.
Results and discussion
Box counts for the pore and the matrix phase are shown for images SEM (Figure 1). According to Eq. (1), for all images the fractal dimensions were obtained as the slope of the loglog plot of measured box counts as a function of box size. The results of all above four SEM images were listed in Table 1.
Table 1. Measured fractal dimension for images SEM.
|
Images |
Measurement |
||||
|
D |
Std. Error of Mean |
Std. Deviation |
Variance |
Correlation coefficient |
|
|
SEM 1 |
1.72 |
0.008 |
0.035 |
0.001 |
0.602 |
|
SEM 2 |
1.74 |
0.022 |
0.110 |
0.012 |
0.788 |
|
SEM 3 |
1.77 |
0.017 |
0.085 |
0.007 |
0.832 |
|
SEM 4 |
1.73 |
0.019 |
0.109 |
0.012 |
0.861 |
The fractal dimensions and correlation coefficients of nano particles were easily obtained by box counting method, as shown in Figures 2 and 3.
According to Eq. (1), for all images the fractal dimensions were obtained as the slope of the loglog plot of measured box counts as a function The fractal dimensions of SEM 1, SEM 2 SEM 3 and SEM 4 images are D=1.72, D=1.74, D=1.77 and D=1.73 respectively.
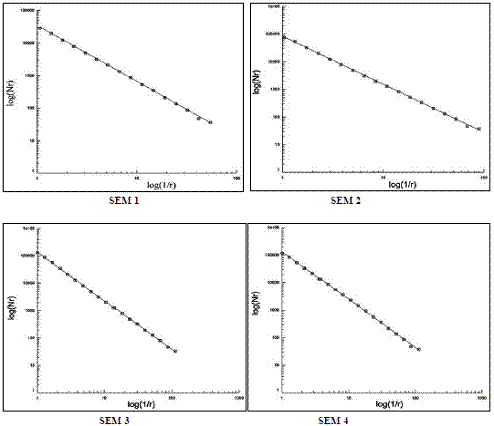
Figure 2. Box counts as measured with images analysis for images SEM
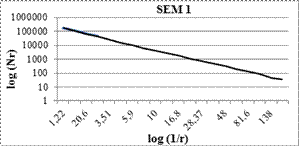
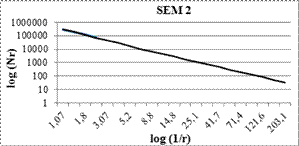
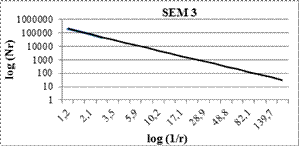
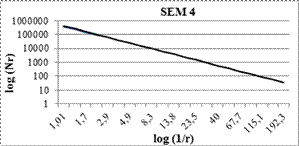
Figure 3.The slope of the linear regression yields the fractal dimensions using measured box counts
Conclusion
The calculation of fractal dimension for surface micro geometry offers a great opportunity for characterization of microscopic images transformed in pixels matrix. The fractal dimension study in this article is based on the box-counting method. Measuring fractal dimensions of a porous medium yields different results depending on the measured feature (pore phase and matrix phase).
References
1. Falconer K., Fractal geometry mathematical foundations and applications, (Second Edition) Great Britain, Cornwall, John Wiley and Sons, 2003, p. 308.
2. Sagan H., Space-Filling Curves, Berlin: Springer-Verlag, 1994, p. 156.
3. Vicsek T., Fractal growth phenomena, Singapore New Jersey: World Scientific, 1992, p. 488.
4. West B. J., Goldberger A. L., Physiology in fractal dimensions, American Scientist, 1987, 75(4), p. 354-365.
5. Milne B. T., Measuring the fractal geometry of landscapes, Applied Mathematics and Computation, 1988, 27(1), p. 67-79.
6. Burrough P. A., Fractal dimensions of landscapes and other environmental data, Nature, 1981, 294, p. 240-242.
7. Rouquerol J., Avnir D., Fairbridge C. W., Everett D. H., Haynes J. H., Pernicone N., Ramsay J. D. F., Sing K. S. W., Unger K. K., Recommendations for the characterization of porous solids (technical report), Pure and Applied Chemistry, 1994, 66(8), p. 1739-1758.
8.
Chang Y., Liu Q., Zhang
J.,
9. Alizadeh-Gheshlaghi E., Shaabani B., Khodayari A., Azizian-Kalandaragh Y., Rahimi R., Investigation of the catalytic activity of nano-sized CuO, Co3O4 and CuCo2O4 powders on thermal decomposition of ammonium perchlorate, Powder Technology, 2012, 217, p. 330-339.
10. Ho C., and Ming-Hsun T., Synthesis and characterization of ZnO nanoparticles having prismshape by novel gascondensation process, Rev. Adv. Mater. Sci, 2008, 18, p. 734-743.
11. Behboudnia M., Habibi-Yangjeh A., Jafari-Tarzanag Y., Khodayari A., Preparation and characterization of monodispersed nano crystalline ZnS in water-rich[EMIM]EtSO4 ionic liquid using ultrasonic irradiation, Journal of Crystal Growth, 2008, 310, p. 4544-4548.
12.
Mandelbrot B. B., The
fractal geometry of nature. W. H. Freeman and Co.,
13. Narine S. S., Marangoni A. G., Relating structure of fat crystal networks to mechanical properties, Food Resources International, 1999, 32, p. 227-248.
14. Baveye P., Boast C. W., Fractal geometry, fragmentation processes and the physics of scale invariance: an introduction. In: Baveye P., Parlange J. Y., Stewart B. A., (Eds.), Fractals in soil science, CRC Press, Boca Raton, 1998, p. 1-54.
15. Lai D., Danca M. F., Fractal and statistical analysis on digits of irrational numbers, Chaos Solitons and Fractals, 2008, 36(2), p.246-252.