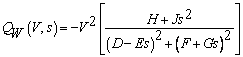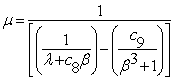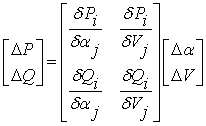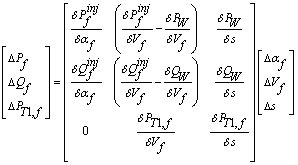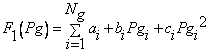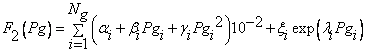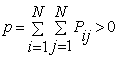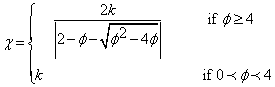Economic/Environmental power dispatch for power systems including wind farms

Imen BEN JAOUED^1*, Tawfik GUESMI² , Yosra WELHAZI³,

and Hsan HADJ ABDALLAH⁴

National Engineering School of Sfax, Sfax University, B.P.W. 3038 Sfax, Tunisia.

E-mails: imenbenjaoued@live.com, tawfik.guesmi@istmt.rnu.tn

yosrawelhazi@yahoo.fr, hsan.haj@enis.rnu.tn

Abstract

This paper presents the problem of the Economic/Environmental power Dispatching (EED) of hybrid power system including wind energies. The power flow model for a stall regulated fixed speed wind generator (SR-FSWG) system is discussed to assess the steady-state condition of power systems with wind farms. Modified Newton-Raphson algorithm including SR-FSWG is used to solve the load flow equations in which the state variables of the wind generators are combined with the nodal voltage magnitudes and angles of the entire network. The EED problem is a nonlinear constrained multi-objective optimization problem, two competing fuel cost and pollutant emission objectives should be minimized simultaneously while satisfying certain system constraints. In this paper, the resolution is done by the algorithm multi-objective particle swarm optimization (MOPSO). The effectiveness of the proposed method has been verified on IEEE 6-generator 30-bus test system and using MATLAB software package.

Keywords

Economic/Environmental power Dispatching (EED); Wind farm; Stall Regulated Fixed Speed Wind Generator (SR-FSWG); Power flow; Newton-Raphson algorithm; Multi-Objective Particle Swarm Optimization (MOPSO)

Introduction

The main objective of the Environmental Economic power Dispatch (EED) consists in the schedule of the power generator units outputs with load demand at minimum operating cost, emissions and pollution while satisfying operational system constraints. A lot of different strategies have been reported in the literature pertaining to the reduction of the atmospheric emissions in power plants [1,2]. These include the use of alternative fuels with a low emission potential, replacement of the existing technologies with energy-efficient ones and emission dispatching [3,4] which is an attractive short-term alternative. In recent years, the environmental and economic concerns have lead to the use of renewable energy resources such as wind power and solar radiation. The use of wind energy conversion systems (WECS) has been considered the most growing renewable energy source [5]. However, the integration of wind generation into the electric power network requires more attention while planning and operating an electrical power system. In the last few decades, different Power Flow (PF) solution techniques such as Gauss-Seidel, Newton-Raphson and Fast decoupled load flow [6] have been developed in order to operate and control the power system. The Newton-Raphson technique is a fundamentally approach for modeling the wind energy systems. This method simultaneously combines the state variables corresponding to the wind generators and the network in a single frame-of-reference.

In literature, several techniques [3,4,7] have been reported in order to handle the EED problem. In recent directions, both fuel cost and emission are considered simultaneously competing objectives. Stochastic search and Fuzzy-based multi-objective optimization techniques have been proposed for the EED problem [7,8]. However, these algorithms are unable to provide a systematic framework for directing the search towards Pareto-optimal front and the extension of these approaches to include more objectives is a very involved question. The EED problem can be also solved by using genetic algorithm based multi-objective techniques [9].

In recent years, multi-objective evolutionary algorithms [10] such as niched Pareto genetic algorithm (NPGA) and strength Pareto evolutionary algorithm (SPEA) algorithms have been used for the EED problem optimization in order to find the optimal solution. Recently, modern meta-heuristic algorithms are used for nonlinear optimization problems. The multi-objective particle swarm optimization (MOPSO) [11] is a typical population-based optimization method. Unlike other heuristic techniques such as genetic algorithm (GA), MOPSO has a flexible mechanism to carry out both global and local search in each iteration process within a short calculation time.

In this paper, MOPSO has proposed to solve the EED problem of hybrid power system including wind energies. In addition, a fuzzy-based mechanism was used in order to extract the best compromise solution. Modified Newton-Raphson algorithm including SR-FSWG was used to solve the load flow equations. To illustrate the effectiveness and potential of the proposed approach to solve the multi-objective EED problem, several runs have been carried out on the IEEE 6-generators 30-bus test system and the results are compared to the recently reported methods. The results show that the proposed approach is efficiently used to solve the EED problem including wind energies and it is superior to other multi-objective methods.

Materials and Method

Modelling of wind generator

At this moment, different types of wind turbine generating units were installed and they can be classified into three categories, namely fixed, semi-variable and variable speed types. This paper addresses the mathematical representation of directly grid-connected wind generators such as SR-FSWG. The idea of this machine is based on an asynchronous squirrel-cage motor generator shown in Figure 1, which is driven by a wind turbine with the stator directly connected to the grid through a power transformer. In this SR-FSWG a fixed shunt capacitor is used to control reactive power compensation.

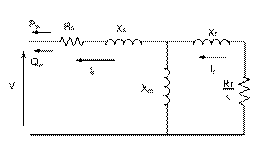
Figure 1. Induction machine equivalent circuit

The power output of this SR-FSWG depends on the turbine and generator characteristics, wind speed, rotor speed and the terminal voltage.

From the equivalent circuit shown in Figure 1, the power converted from mechanical to electrical form P_g can be represented by (1).

(1)

where R_r is the rotor resistance, s is the slip of the induction generator and I_r is the rotor current given by the following equation :

(2)

The active and reactive powers, determined by equations (3) and (4), are dependent on the machine’s slip s and the terminal voltage V.

	(3)
	(4)

where the variables are given in [12].

The wind turbine mechanical power output P_m [W] extracted from the wind by this generator [13] can be written as

(5)

were ρA [g/m³] is the density of air, Vw [m/s] is the wind speed, [m²] is the area swept by the rotor and Cp(λ,β) is the power coefficient. The Cp given by (6) is a nonlinear function of the tip speed ratio λ and the pitch angle β:

(6)

where, depends on the wind speed Vw and the radius of the rotor R [m] as given in (7).

(7)

where W_r [rad/s] is the angular speed of the turbine and μ is given in (8):

(8)

μ is represented by (8), [degrees] is the pitch angle and the constants C1 to C9 are the parameters of design of the wind turbine

Power flow model

The objective of this section is to give a power flow model for a power system without and with wind farm device.

Power flow analysis without wind farm

The injected real and reactive power flow at bus, for power system with N buses, can be written as in [14]:

	(9)
	(10)

where V_i and α_i are respectively, modulus and argument of the complex voltage at bus I_. Y_ij and θ_ij are respectively, modulus and argument of the ij -th element of the nodal admittance matrix Y. The resolution of the problem of power flow uses the Newton-Raphson method [14]. The nonlinear system is represented by the linearized Jacobian equation given by the following equation:

(11)

Power flow analysis with wind farm

When the SR-FSWG is connected at terminal bus f of the system, the set of mismatch power flow equations is

	(12)
	(13)

where P_lf and Q_lf represent the active and reactive powers drawn by the load at bus f

	(14)
	(15)

P_f^inj and Q_f^inj are active and reactive power injections at bus f, G_f and B_f are transfer conductance and susceptance between buses f and i respectively.

The power balance inside the induction machine is represented by (16).

(16)

Finally, the modified power flow equations can be solved with the Newton-Raphson method by using equation (17).

(17)

Problem formulation

The OPF is a mathematical optimization problem set up to minimize a multi-objective function subject to equality and inequality constraints.

Objective Functions

The EED problem is to minimize two competing objective functions, fuel cost and emission, while satisfying several equality and inequality constraints. It can be considered as a nonlinear multi-objective problem (MOP). The objectives functions are [9,15].

· Fuel Cost Function

(18)

where a_i, b_i and c_i are the cost coefficients of the i-th generator and N_g is the number of generators committed to the operating system. is the output power of the i-th generator.

· Emission Function

(19)

where α_i, β_i, γ_i, ξ_i and λ_i are the emission coefficients of i-th generator

Problem constraints

In this manuscript, the equality and inequality constraints of the problem are as follows.

· Production capacity constraints

The generated real power of each generator at the bus i is restricted by lower limit p_g^max and upper limit p_g^max :

(20)

· Active power loss constraint:

Active power losses p of the transmission and transport lines, are positives:

(21)

· Load flow constraints

	(22)
	(23)

where P_Gi and Q_Gi are generated real and reactive powers at bus i, respectively. P_Di and Q_Di are respectively, real and reactive power loads at bus i. P_i and Q_i are respectively the injected real and reactive power flow at bus i

· Line flow constraints :

This constrains can be described as:

(24)

where P_l the real power flow of line. P_l^max is the power flow up limit of line l and N_L is the number of transmission lines.

The MOPSO technique

This approach is population-based, it uses an external memory, called repository, and a geographically-based approach to maintain diversity. MOPSO is based on the idea of having a global repository in which every particle will deposit its flight experiences after each flight cycle. The general algorithm of MOPSO can be described as follows [11]:

Step 1: Initialize an array of particles with random positions POP and their associated velocities VEL.

Step 2: Evaluate the fitness function of each particle.

Step 3: Store the positions of the particles that represent nondominated vectors in the repository REP.

Step 4: Generate hypercubes of the search space explored so far, and locate the particles using these hypercubes as a coordinate system.

Step 5: Initialize the memory of each particle.

Step 6: Compute the speed of each particle using the following expression:

(25)

where φ₁ and φ₂ are weights affecting the cognitive and social factors, respectively. r₁ and r₂ are random numbers in the range [0-1]. χ is the constriction factor that ensures convergence which is calculated as in (26)

	(26)
where 0<k<1 and ϕ= φ1 +φ2	(27)

PBEST(i) is the best position that the particle i has had; REP(h) is a value that is taken from the repository; the index h is selected by applying roulette-wheel selection

Step 7: Update the position for each particle

POP(i)=POP(i)+REP(i)

(28)

Step 8: Maintain the particles within the search.

Step 9: Evaluate each of the particles in POP.

Step 10: Update the contents of REP together with the geographical representation of the particles within the hypercubes.

Step 11: Update the particle’s position using Pareto dominance.

Step 12: Repeat Step 6-11 until a stopping criterion is satisfied or the maximum number of iterations is reached.

Results and Discussion

The effectiveness of the proposed algorithms is tested using IEEE 30 bus system including wind farms comprising ten wind generators. Data and results of system are based on 100 MVA. Bus 30 is the slack bus. The test system data can be found in [16].

The values of fuel cost and emission coefficients corresponding to the generators, G_i are shown in [17]. The bounds of generated powers are: P_gi^min=0.05 p.u. and P_gi^max=1.5 p.u.

The initial value for the slip of the induction generator to execute simulations is given by s(0)=s_nom/2, where s_nom=-0.005 The value of fixed capacitors installed at each wind generator is 30% of rated power. The induction generator circuit parameters are given in [12].

Power flow of base case

Table 1 shows the voltage magnitudes and angles given by the power flow program for the system without and with wind farm. However, slip, active and reactive powers given by ten SR_FSWG is also the outputs of power flow program of the system with wind farm.

The results assuming that wind speed is V_w=10 m/s at all wind farms. The active power requested (PD) is .

The convergence characteristic, of the power flow program without and with wind farm is given in Figure 2.

Table 1. Solution of the power flow program for the base case

Bus No	Without wind farm		With wind farm
	[pu]	[Degree]	[pu]	[Degree]
1	0.9568	-18.4720	0.9569	-11.5578
2	0.9697	-17.5551	0.9698	-10.6411
3	1.0067	-11.9744	1.0105	-5.7416
4	0.9878	-16.1597	0.9880	-9.2461
5	0.9608	-17.1391	0.9617	-9.7909
6	0.9792	-16.6855	0.9801	-9.3381
7	0.9796	-17.0775	0.9822	-9.0301
8	0.9920	-17.1170	0.9955	-8.5782
9	0.9935	-16.7448	0.9959	-8.6576
10	0.9930	-16.7642	0.9954	-8.6738
11	1.0028	-17.1434	1.0057	-8.8268
12	0.9992	-17.7798	1.0022	-9.2322
13	1.0002	-17.6750	1.0033	-9.0559
14	1.0047	-16.4141	1.0072	-8.2195
15	1.0133	-16.2660	1.0171	-7.5764
16	1.0078	-16.8697	1.0121	-7.9755
17	1.0133	-16.7887	1.0189	-7.7447
18	1.0293	-15.8452	1.0351	-6.6557
19	1.0064	-16.2977	1.0087	-8.2003
20	1.0264	-14.5852	1.0290	-6.4553
21	1.0025	-13.1126	1.0055	-7.1430
22	1.0113	-11.3614	1.0162	-5.3686
23	1.0169	-9.6984	1.0251	-4.5893
24	1.0245	-8.0293	1.0318	-3.7798
25	1.0710	-15.8452	1.0710	-4.1010
26	1.0820	-14.5852	1.0820	-4.5152
27	1.0100	-12.0944	1.0100	-5.5252
28	1.0100	-14.3647	1.0100	-8.5163
29	1.0450	-5.5222	1.0450	-2.3737
30	1.0600	0	1.0600	0
s	-		-0.0029
10.Pw [MW]	-		6.3291
10.Qw [MVAR]	-		-1.5165

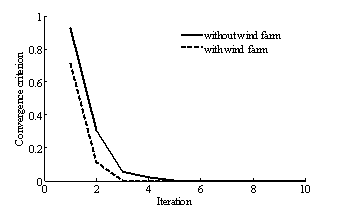
Figure 2. Convergence criterion of the power flow algorithm

Optimal solutions

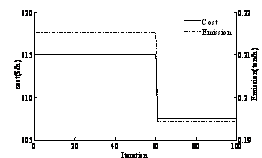
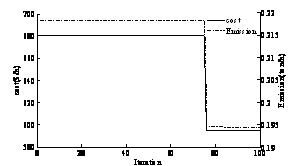
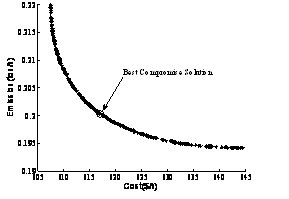
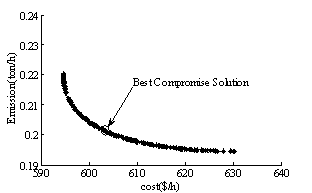
In order to demonstrate the effectiveness of the MOPSO to solve the EED problem a compromise with two multiobjective evolutionary algorithms (MOEA) such as NSGA and SPEA [10] has been done in this study. Two cases without and with wind farm have been considered. The convergence of objective functions and Pareto optimal fronts are given respectively in Figure 3 and 4.

· Without wind farm

Table 2.The best solution without wind farm

	without wind farm
	Best cost			Best Emission
	NPGA	SPEA	MOPSO	NPGA	SPEA	MOPSO
cost [$/h]	620.46	619.60	607.52	657.59	651.71	644.33
Emission[ton/h]	0.2243	0.2244	0.2198	0.2017	0.2019	0.1942
Pg1 [pu]	0.1127	0.1319	0.1117	0.4753	0.4419	0.4110
Pg2  [pu]	0.3747	0.3654	0.3097	0.5162	0.4598	0.4583
Pg3  [pu]	0.8057	0.7791	0.5954	0.6513	0.6944	0.5438
Pg4  [pu]	0.9031	0.9282	0.9778	0.4363	0.4616	0.3933
Pg5  [pu]	0.1347	0.1308	0.5227	0.1896	0.1952	0.5502
Pg6  [pu]	0.5331	0.5292	0.3486	0.5988	0.6131	0.5072

Table 3 gives the best compromise solution extracted using membership functions [10]. It is clear that the MOPSO has the best results compared to NPGA and SPEA.

Table 3. Best compromise solutions without wind farm

	without wind farm
	NPGA	SPEA	MOPSO
cost [$/h]	630.06	629.59	616.9529
Emission[ton/h]	0.2079	0.2079	0.2004

(a)	(b)

Figure 3. Convergence of cost and emission objective functions: (a) without wind form,(b) with wind form

(a)	(b)

Figure 4. Pareto front using MOPSO: (a) without wind farm, (b) with wind farm

· With wind farm

In this study, the wind farms comprising ten wind generators is connected in bus 24 of the IEEE 30 bus system . The results of simulation are given in Table 4.

Table 5 gives the best compromise solution. From the results, it can be seen that the fuel cost, is reduced by connect the wind farm.

Table 4. The best solution with wind farm of MOPSO

	MOPSO with wind farm
	Best cost	Best Emission
cost [$/h]	594.6563	630.2102
Emission [ton/h]	0.2203	0.1945
Pg1 [pu]	0.1009	0.3951
Pg2 [pu]	0.2963	0.4431
Pg3 [pu]	0.7140	0.5914
Pg4 [pu]	0.9318	0.3642
Pg5 [pu]	0.4335	0.5226
Pg6 [pu]	0.3224	0.4828

Table 5.Best compromise solutions with wind farm of MOPSO

Cost [$/h]	603.0989
Emission[ton/h]	0.2014

Conclusions

A modified Newton-Raphson algorithm for load flow including SR_FSWG is developed. The efficiency of the proposed MOPSO algorithm to solve multi-objective EED problem is verified by comparison with NPGA and SPEA algorithms. IEEE-30-bus 6-generators is considered in simulation results.

References

1. El-Keib A. A., Ma. H, Hart J. L., Economic dispatch in view of the clean air act of 1990, IEEE Trans. Power Syst., 1994, 9, p. 972-978.

2. Talaq J. H., El-Hawary F., El-Hawary M. E., A summary of environmental/economic dispatch algorithms, IEEE Trans. Power Syst., 1994, 9, p. 1508-1516.

3. Dhillon J. S., Parti S. C., Kothari D. P., Stochastic economic emission load dispatch, Electric Power Syst. Res., 1993, 26, p. 186-197.

4. Chang C. S., Wong K. P., Fan B., Security-Constrained multiobjective generation dispatch using bicriterion global optimization, Proc. Inst. Elect. Eng.-Gen. Transm., 1995, 142(4), p. 406-414.

5. World Wind Energy Report 2009, WWEC, Istanbul, Turkey, 2010 March, http://www.wwindea.org/home/images/stories/worldwindenergyreport 2009s.pdf

6. Stevenson W. D., Elements of Power System Analysis, McGraw-Hill, 1982.

7. Huang C. M., Yang H. T. Huang, C. L., Bi-objective power dispatch using fuzzy satisfaction maximizing decision approach, IEEE Trans. Power Syst., 1997, 12(4), p. 1715-1721.

8. Das D. B., Patvardhan C., New multi-objective stochastic search technique for economic load dispatch, IEE Proc. Gener. Transm. Distrib., 1998, 145(6), p. 747-752.

9. Abido M. A., A novel multiobjective evolutionary algorithm for environmental/economic power dispatch, Electric Power Syst. Res., 2003, 65, p. 71-81.

10. Abido M. A., Multiobjective Evolutionary Algorithms for Electric Power Dispatch Problem, IEEE Transactions on Evolutionary Computation, 2006, 10(3), p. 315-329.

11. Carlos A., Coello C., Lechuga M. S., MOPSO: A Proposal for Multiple Objective Particle Swarm Optimization, IEEE Transactions on Evolutionary Computation, 2002, 2(3), p. 1051-1056.

12. Castro L. M., Fuerte-Esquivel C. R., Tovar-Hernández J. H., A unified approach for the solution of power flows in electric power systems including wind farms, Electric Power Systems Research, 2011, 81, p. 1859-1865.

13. Heier S., Grid Integration of Wind Energy Conversion Systems, John Wiley and Sons, 1998.

14. Marouani I., Guesmi T., Hadj Abdallah H., Ouali A., Optimal Reactive Power Dispatch Incorporating UPFC Devices using NSGA II Approach, Science Academy Transactions on Renewable Energy Systems Engineering and Technology, 2011, 1(1).

15. Samir S., Khaled Z., Economic Load Dispatch with Security Constraints of the Algerian Power System using Successive Linear Programming Method, Leonardo Journal of Sciences, 2006, 9, p. 73-86.

16. Tawfik Guesmi, Hsan Hadj Abdallah, Ahmed Toumi, New Approach to Solve Multiobjective Environmental / Economic Dispatch, J. Electrical Systems, 2006, 2, p. 64-81.

17. Saoussen B., Hsan Hadj A., Abderrazak O., Economic Dispatch for Power System included Wind and Solar Thermal energy, Leonardo Journal of Sciences, 2009, 14, p. 204-220.