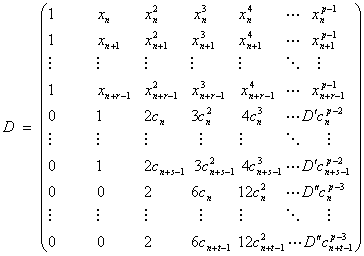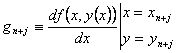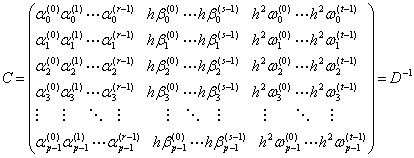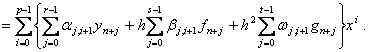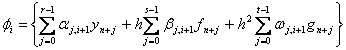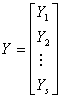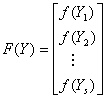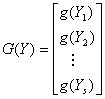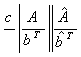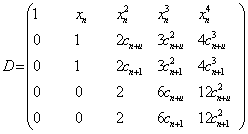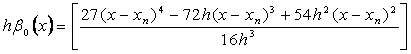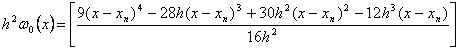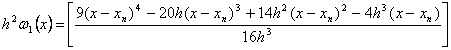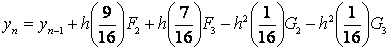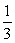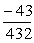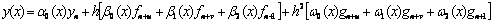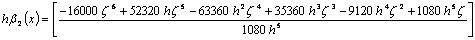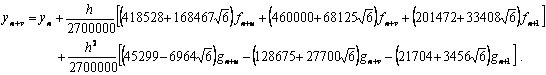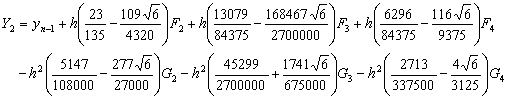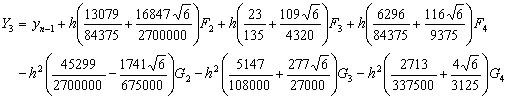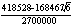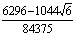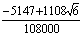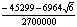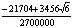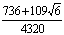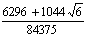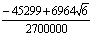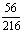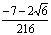Application of second derivative Runge-Kutta collocation methods to stiff systems of initial value problems
Samaila MARKUS1 and Dauda Gulibur YAKUBU2*
1Department of Mathematics and Statistics, University of Maiduguri, PMB 1069, Maiduguri, Borno State, Nigeria
2Department of Mathematical Sciences, Abubakar Tafawa Balewa University, PMB 0248, Bauchi, Bauchi State , Nigeria
E-mails: daudagyakubu@gmail.com &smvalleh@gmail.com
*Corresponding author: Phone: 2348134168950 & 2348052168433
Abstract
In this paper we consider the construction of implicit second derivative Runge-Kutta collocation methods designed for the continuous numerical solution of stiff systems of first order initial value problems in ordinary differential equations. These methods are obtained based on the multistep collocation technique, which are shown to be convergent, with improved regions of absolute stability. Although the implementation of the second derivative Runge-Kutta collocation methods remains iterative due to the implicit nature of the methods, the advantage gained makes them suitable for solving stiff systems with eigenvalues of large modulus lying close to the imaginary axis. Some absolute stability characteristics and order of accuracy of the methods are studied. Finally, we show two possible ways of implementing the methods and compare them on some numerical examples found in the literature to demonstrate the high order of accuracy and reliability of the methods.
Keywords
Block hybrid scheme; Continuous scheme; Multistep collocation formula; Second-derivative Runge-Kutta method; Stiff system
Introduction
In the past few decades many authors proposed different numerical integration methods to obtain more accurate approximate solution to ordinary differential equations (ODEs), especially stiff systems of initial value problems in ordinary differential equations. However, extensive numerical experiments have shown that implicit integrators have the numerical superiority over the explicit methods when applied to solve stiff systems of ODEs [1-4]. In particular, implicit Runge-Kutta methods play an important role in the numerical solution of stiff systems of ODEs, because they have good stability properties and high order of convergence. In this paper we derive implicit second-derivative Runge-Kutta (SDRK) collocation methods designed for the continuous numerical solution of stiff systems of initial value problems in ODEs of the form
|
|
(1.1) |
Here the unknown function y is a mapping y:[xo,T]®Rd and the right-hand side function f is f:[x0,T]xRd®Rd which is assumed to be sufficiently smooth, y0®Rd is the given initial value and dy/dx is the differential operator. Let h>0 be a constant step size and we define the grid by xn=x0+nh, n=0,1,2,..,N where Nh=T-x0and a set of uniformly spaced points on the integration interval is defined by x0<x1<x2<…..<xn+1=T The main reason for considering the second derivative terms is to derive a set of methods which are suitable for the continuous numerical solution of stiff differential systems with Jacobians having large eigenvalues lying close to the imaginary axis. However, for some important classes of problems it is necessary, for the sake of efficiency, to allow second-derivative integration methods to be used (see [5-8]) and in this case existing numerical methods tend to be much less satisfactory. Further, we will examine in detail the problem of implementing the second-derivative Runge-Kutta integration methods with fixed time steps. We show that, even though enormous gains in efficiency can be achieved if the methods are implemented in an appropriate way, there are still some important practical problems to be overcome, for example, the calculation of the second derivative terms in the methods which costs little higher than the first derivative terms [9].
There are several eminent authors who derived methods that can handle non-stiff, stiff, periodic and oscillatory problems handy [2-4,9], but little seems to have been done in deriving implicit second-derivative Runge-Kutta collocation methods with minimal function evaluations, uniformly accurate orders and maximal gain in efficiency. Hence, these motivate us to consider the construction of the implicit second derivative Runge-Kutta collocation methods in this paper.
Definition 1.1: A numerical method is said to be A(α)-stable αÎ(0,π/2) if its region of absolute stability contains the infinite wedge Wα where
|
|
see [10]. |
Theorem 1.1: If f satisfies Lipschitz condition with constant L then the initial value problem y’(x)=f(x,y(x)), y(x0)=y0 possesses a unique solution on the interval [x0, T] see [11].
Definition 1.2: A solution y(x) of (1.1) is said to be stable if given any Î>0 there is δ>0such that any other solution y(x) of (1.1) which satisfies
|
|
(1.2a) |
also satisfies
|
|
(1.2b) |
for all x>a.
The solution y(x) is asymptotically stable if in addition to (1.2b) as x®∞.
Material and method
The implicit second derivative Runge-Kutta collocation methods
In this section our objective is to describe the construction of the implicit second-derivative Runge-Kutta collocation methods based on the multistep collocation technique. In this regard we seek an approximate solution to the exact solution of (1.1) by the interpolant of the form
|
|
(1.3) |
which is twice continuously differentiable. We set the sum r+s+t to be equal to p so as to be able to determine {αi} in (1.3). In this formulation r denotes the number of interpolation points used and s>0, t>0are distinct collocation points. Interpolating (1.3) at the points {xn+j}, and collocating y’(x) and y”(x) at the points {cn+j} we obtain the following system of equations
|
|
(1.4) |
|
|
(1.5) |
|
|
(1.6) |
In fact equations (1.4) to (1.6) can be expressed in the matrix-vector form as
|
|
(1.7) |
where the p-square matrix D, p- vectors α and y are defined as follows:
|
|
(1.8) |
|
|
|
where D’=(p-1) and D’’=(p-1)(p-2) in (1.8) represent the first and second derivatives respectively and correspond to the differentiation with respect to x. Similar to the Vandermonde matrix, the matrix D in (1.7) is non-singular. Consequently, equation (1.7) has the unique solution given by
α=Cy where C=D-1 (1.9)
Rearranging equations (1.7) to (1.9) we obtain the multistep collocation formula of the type in [12] which was a generalization of [13] and here we extend to second derivative as follows.
|
|
(1.10) |
|
where: |
|
|
|
|
|
|
|
|
|
|
Here αj(x), βj(x), ωj(x) are continuous coefficients of the method which are to be determined. They are assumed polynomials of the form
|
|
(1.11) |
|
|
|
|
|
The numerical constant coefficients αj,i+1, βj,i+1, ωj,i+1 in (1.11) are to be determined.
In fact, the above coefficients can be obtained from the components of the matrix D-1.
That is, if the identity (1.12) holds. Actual evaluations of the matrices C and D are carried out with a computer algebra system, for example, Maple, to determine the constant coefficients αj,i+1, βj,i+1, and ωj,i+1 in (1.11).
|
|
(1.12) |
To obtain the continuous scheme, we insert (1.11) into (1.10) to have
|
|
(1.13) |
|
|
|
|
|
|
|
where: |
|
|
|
|
From (1.13) we have
|
|
(1.14) |
|
|
|
|
|
Recall that p=r+s+t, such that (1.14) reduces to
|
|
(1.15) |
Thus, expanding (1.15) fully we obtain the proposed continuous scheme as follows:
![]() (1.16)
(1.16)
where T denotes transpose of the matrix C in (1.12) and the vector (1,x,x2,…,xr+s+t-1).
Remark 1.
We call D the multistep collocation and interpolation matrix which has a very simple structure. From (1.8), the columns of D which give the continuous coefficients αj(x), βj(x), ωj(x) can be obtain from the corresponding columns of C. As can be seen the entries of C are the constant coefficients of the polynomial given in (1.11) which are to be determined. The matrix C is the solution vector (output) and D is termed the data (input), which is assumed to be non-singular for the existence of the inverse matrix C.
In the second-derivative methods, we see that not only the function f(x,y) is evaluated at some intermediate points, but in addition the functions Df, D2f where Dis the differential operator (see [14]). Hence, in addition to the computation of the f-values at the internal stages in the standard Runge-Kutta methods, the modified methods involve computing g-values, where f and g are as defined in (1.10).
According to [15] these methods can be practical if the costs of evaluating g are comparable to those in evaluating f and can even be more efficient than the standard Runge-Kutta methods if the number of function evaluations is fewer. It is convenient to rewrite the coefficients of the defining formula (1.10) evaluated at some certain points in the block matrix form as,
|
|
(1.17a) |
|
|
(1.17b) |
where A=[aij]sxs, Â=[âij]sxs
indicate the dependence of the stages on the derivatives found on the other
stages and b=[bi]sx1, ![]() are vectors of quadrature weights showing how the final result
depends on the derivatives computed at the various stages, I is the identity
matrix of size equal to the differential equation system to be solved and N is
the dimension of the system. Also Ä is the Kronecker product of two matrices. For
simplicity, we write the method in (1.17) as follows:
are vectors of quadrature weights showing how the final result
depends on the derivatives computed at the various stages, I is the identity
matrix of size equal to the differential equation system to be solved and N is
the dimension of the system. Also Ä is the Kronecker product of two matrices. For
simplicity, we write the method in (1.17) as follows:
|
|
(1.18a) |
|
|
(1.18b) |
and the block vectors in RsN are defined by
|
|
|
|
(1.19) |
The coefficients of the implicit second-derivative Runge-Kutta collocation methods can be conveniently represented more compactly in an extended partitioned Butcher Tableau, of the form
|
|
(1.20) |
where c=[1]sx1 is the abscissae vectors which indicates the position within the step of the stage values.
Specification of the implicit second derivative Runge-Kutta collocation methods
A fourth-order implicit second derivative Runge-Kutta collocation method
In this section we develop the general form of conditions for the coefficients of the implicit second-derivative Runge-Kutta collocation methods. To obtain the coefficients of the first method, the matrix D in (1.8) takes the form,
|
|
(1.21) |
Inverting the matrix D in (1.21) once, we obtain the continuous scheme of the form in (1.16) as follows
|
|
(1.22) |
where
|
|
|
|
|
|
|
|
|
|
To get the value of u in (1.21), we find the zero of the Nth degree Jacobi polynomial (see, [16]) defined by
|
|
(1.23a) |
where
|
|
(1.23b) |
with γ0=1.
Next by substituting u = ⅓ into the continuous scheme (1.22) and evaluate at x=xn+1 and xn+u we obtain the following block hybrid discrete scheme, which can be applied simultaneously as block method for dense output, if desired,
|
|
(1.24a) |
|
|
(1.24b) |
If we convert the block hybrid discrete scheme (1.24(a-b)) to implicit second-derivative Runge-Kutta collocation method and write the method in the form of (1.18) we have the following
|
|
(1.25) |
The internal stage values at the nth step are calculated as,
|
|
|
|
|
|
|
with the stage derivatives as follows: |
|
|
|
|
|
|
A sixth-order implicit second derivative Runge-Kutta collocation method
Here we derive implicit second-derivative Runge-Kutta collocation method of higher order for the numerical solution of stiff systems. The matrix D in (1.8) takes the following form
|
|
(1.26) |
where u and v are the zeros of p2(x)=0. Jacobi polynomial in (1.23)
of degree ![]() which are
valid in the interval [xn,xn+1]. Inverting the matrix in
(1.26) once we obtain the continuous scheme as follows:
which are
valid in the interval [xn,xn+1]. Inverting the matrix in
(1.26) once we obtain the continuous scheme as follows:
|
|
(1.27) |
where
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Evaluating the continuous scheme (1.27) at the points {xn+1,xn+u,xn+v} we obtain the block hybrid discrete scheme which can also be applied simultaneously as block method for dense output, if desired,
|
|
|
|
|
(1.28) |
|
|
|
Writing the method in the formalism of (1.18) we have
|
|
(1.29) |
The internal stage values at the nth step are calculated as,
|
|
|
|
|
|
|
|
where the stage derivatives are as follows:
|
|
|
|
|
|
|
|
Analysis of the properties of the implicit SDRK collocation methods
Order, Consistency, Zero-Stability and Convergence of the Implicit SDRKCMs
With the multi-step collocation formula (1.10) we
associate the linear difference operator ![]() defined
by:
defined
by:
|
|
(1.30) |
where y(x) is an arbitrary function, continuously differentiable on [x0, T]. Following [17], we can write the terms in (1.30) as a Taylor series expansion about the point x to obtain the expression,
|
|
(1.31) |
where the constant coefficients Cp, p = 0,1,2,… are given as follows:
|
|
|
|
|
|
|
|
According to [17], the multistep collocation formula (1.10) has order p if
|
|
(1.32) |
Therefore, Cp+1 is the error constant and Cp+1hp+1y(p+1)(xn) is the principal local truncation error at the point xn (see [18]). Hence from our calculation the order and error constants for the constructed methods are presented in Table 1. It is clear from the Table that the implicit second-derivative Runge-Kutta collocation methods are of high-order. They have smaller error constants and hence more accurate than the conventional Radau-Runge-Kutta methods of the same order of convergence.
Table 1. Order and error constants of the implicit SDRK collocation methods
|
Method |
Order |
Error constant |
|
Method (1.25) |
P=4 |
C5=9.8765 |
|
Method (1.29) |
P=6 |
C7=2.5714 |
Definition 1.3: Consistency
A linear multistep method is said to be consistent if the order of the method is greater or equal to one, that is if p>1 (see, [17]).(i) ρ(1)=0 and(ii)ρ’(1)=σ(1), where ρ(z) and σ(z) are respectively the 1st and 2nd characteristic polynomials.
From Table 1 and definition 1.3, we can attest that the implicit second-derivative Runge-Kutta collocation methods are consistent.
Definition 1.4: Zero-stability
A linear multistep method is said to be zero-stable if the roots:
|
|
|
|
|
|
see [17].
Based on definition 1.4, the newly constructed implicit second-derivative Runge-Kutta collocation methods are zero-stable.
Definition 1.5: Convergence
The necessary and sufficient conditions for a linear multistep method to be convergent are that it must be consistent and zero-stable (see [10]). Hence, from definitions 1.3 and 1.4 the implicit second-derivative Runge-Kutta collocation methods are convergent.
Regions of absolute stability of the implicit SDRK collocation methods
To study the stability properties of the implicit second-derivative Runge-Kutta collocation methods we reformulate them as general linear methods (see [19]). Hence, we use the notations introduced by [20] which a general linear method is represented by the partitioned (s+r)×(s+r) matrix, (containing A, U, B, V),
|
|
(1.33a) |
where
|
|
|
|
|
|
|
|
|
|
and e=[1,…,1]tÎR. Hence (1.33a) takes the form
|
|
(1.33b) |
where r denotes quantities as output from each step and input to the next step and s denotes stage values used in the computation of the step y1,…,ys. The coefficients of these matrices indicate the relationship between the various numerical quantities that arise in the computation of stability regions. The elements of the matrices A, U, B and V are substituted into the stability matrix. In the sense of [21] we apply (1.33) to the linear test equation y’=λy,x>0 and λÎC but for the second-derivative high-order methods we use y’’=λ2y which leads to the recurrence relation y[n+1]=M(z)y[n], n=1,2,…,N-1, z=λh, where the stability matrix M(z) is defined by
|
|
(1.34) |
We also define the stability polynomial p(η,z) by the relation
|
|
(1.35) |
and
the absolute stability region ![]() of
the method is given by
of
the method is given by
|
|
To compute the regions of absolute stability we substitute the elements of the matrices A, U, B and V into the stability function (1.34) and finally into the stability polynomial (1.35) of the methods, which is plotted to produce the required graphs of the absolute stability regions of the methods as shown in Figure 1.
|
|
|
Method
(1.25) is A( |
|
Method(1.29)
is A( |
Figure 1. Regions of absolute stability of the implicit SDRK collocation methods
The methods constructed in this paper are A(α)-stable, since their regions consist of the complex plane outside the enclosed Figures, with only very small portion inside the left hand-half plane.
Numerical experiments
Our aim in this section is to compare the performance of the new methods with other methods of the conventional type (Radau methods) which are widely known to be among the most efficient methods for the numerical solution of stiff ordinary differential equations. Therefore, we report the numerical results obtained from the applications of the new implicit second-derivative Runge-Kutta collocation methods. We present the computed results in the formalism of [22]. In the presentation we use nfe to denote the number of function evaluations and Ext to indicate the exact solutions.
Example 1. Consider the stiff system of first order differential equation,
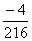
The exact solution is
![]()
This system has eigenvalues of large modulus lying close to the imaginary axis -1±15i. We solve the system in the range of [0, 50] with h = 0.1and the results obtained are shown in Table 2. In this example we compare the results from the two new methods side by side in the Table. The solution curves obtained are compared with the exact (Ext) solutions in Figure 2. Thus, for fair comparison see the results from the third derivative methods of [23] Table 4 page 447 and results of [24] Table 2 page 166.
Table 2. Absolute errors in the numerical integration of example 1
|
x |
Yi |
Method (1.25) |
Method (1.29) |
|
5 |
Y1 |
3.46368813864673 ×10-3 |
2.16834805259769 ×10-3 |
|
Y2 |
3.94364780750056 ×10-4 |
6.23671456063679 ×10-4 |
|
|
50 |
Y1 |
1.49495218771792 ×10-4 |
7.38442455972734 ×10-5 |
|
Y2 |
4.86742095474412 ×10-9 |
2.19934956374418 ×10-9 |
|
|
150 |
Y1 |
1.85517639473028 ×10-4 |
1.20177414793520 ×10-4 |
|
Y2 |
1.45786198883123 ×10-8 |
7.02697714351372 ×10-9 |
|
|
250 |
Y1 |
1.25223273382179 ×10-13 |
1.99479371074799 ×10-14 |
|
Y2 |
8.66743589934986 ×10-13 |
3.55424556071686 ×10-13 |
|
|
500 |
Y1 |
1.64891543846432 ×10-23 |
2.32684011997371 ×10-24 |
|
Y2 |
4.31480861603385 ×10-24 |
3.70791674680754 ×10-24 |
a)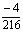 b)
b)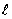
Figure 2. Graphical plots of example 1 using Second Derivative Runge-Kutta Collocation methods: a) Solution curve of example 1 using method (1.25), with nfe =500; b) Solution curve of example 1 using method (1.29), with nfe =500
Example 2: The second example is a stiff linear system of equation, see [25],
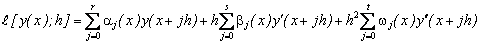
The exact solution is given by
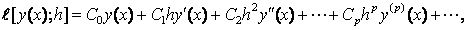
We solve this system in the range [0, 10]. In this example we also compare the results from the two new methods in Table 3 and the efficiency curves obtained are compared with the exact solutions in Figure 3.
Table 3. Absolute errors in the numerical integration of example 2
|
x |
Yi |
Method (1.25) |
Method (1.29) |
|
5 |
Y1 |
7.00794977603891 × 10-12 |
2.22044604925031 × 10-16 |
|
Y2 |
7.04547531427124 × 10-12 |
0 |
|
|
50 |
Y1 |
2.27042828981894 × 10-11 |
1.11022302462516 × 10-15 |
|
Y2 |
2.27533547558778 × 10-11 |
1.11022302462516 × 10-15 |
|
|
150 |
Y1 |
7.35667637918880 × 10-11 |
4.44089209850063 × 10-16 |
|
Y2 |
7.35377314597940 × 10-11 |
3.33066907387547 × 10-16 |
|
|
250 |
Y1 |
4.08534317486442 × 10-11 |
1.11022302462516 × 10-16 |
|
Y2 |
4.08287292863463 × 10-11 |
1.11022302462516 × 10-16 |
|
|
500 |
Y1 |
6.84553524976650 × 10-11 |
5.55111512312578 × 10-16 |
|
Y2 |
6.84068357514889 × 10-11 |
5.55111512312578 × 10-16 |
a)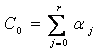 b)
b)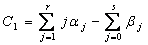
Figure 3. Graphical plots of example 2 using second derivative Runge-Kutta collocation methods: a) Solution curve of example 2 using method (1.25), with nfe =500;b) Solution curve of example 2 using method (1.29), with nfe =500
Example 3: The third test example is a stiff problem taken from [25].
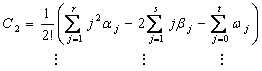
The exact solution is,
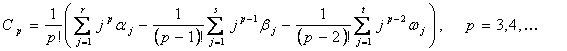
The eigenvalues of the system are λ1=-50 and λ2,3 = 0.1±8i. The computed solutions of the example within the interval of [0, 1] are presented in Table 4 and the graphical plots are shown in Figure 4.
Example 4: We consider another linear problem which is particularly referred to by [27] as a troublesome problem for some existing methods because the eigenvalues of this problem are lying close to the imaginary axis where some stiff integrators were known to be inefficient. The eigenvalues of the Jacobian are λ1,2 = -10±100i, λ3 = -4, λ4 = -1, λ5 = -0.5 and λ6 = -0.1.
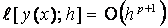
Table 4. Absolute errors in the numerical integration of example 3
|
x |
Yi |
Radau IIA method [20, 26] |
Method (1.29) |
|
5 |
Y1 |
3.70353636647280 × 10-10 |
3.12638803734444 × 10-13 |
|
Y2 |
3.70363018031838 × 10-10 |
3.12583292583213 × 10-13 |
|
|
Y3 |
3.70344199751571 × 10-10 |
3.12638803734444 × 10-13 |
|
|
50 |
Y1 |
4.98715513330694 × 10-11 |
4.27435864480685 × 10-14 |
|
Y2 |
5.00358643407139 × 10-11 |
4.27435864480685 × 10-14 |
|
|
Y3 |
4.97826224687969 × 10-11 |
4.21884749357559 × 10-14 |
|
|
150 |
Y1 |
2.59459120854899 × 10-13 |
8.88178419700125 × 10-16 |
|
Y2 |
2.37143638059933 × 10-13 |
5.99520433297585 × 10-15 |
|
|
Y3 |
1.55916946020795 × 10-14 |
6.77236045021345 × 10-15 |
|
|
250 |
Y1 |
4.30766533554561 × 10-13 |
7.10542735760101 × 10-15 |
|
Y2 |
4.39759340054025 × 10-13 |
2.88657986402541 × 10-15 |
|
|
Y3 |
8.70636895911048 × 10-13 |
4.44089209850063 × 10-15 |
|
|
500 |
Y1 |
1.29318777908338 × 10-12 |
5.99520433297585 × 10-15 |
|
Y2 |
9.13435993510348 × 10-14 |
8.93729534823251 × 10-15 |
|
|
Y3 |
1.20203846876166 × 10-12 |
3.55271367880050 × 10-15 |
a) 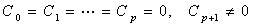 b)
b)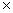
Figure 4. Graphical plots of example 3 using Radau IIA method [20,26] and SDRKC method: a) Solution curve of example 3 using Radau IIA method [20,26], with nfe =500, b) Solution curve of example 3 using method (1.29), with nfe =500
We solve this problem in the range 0 ≤ x ≤ 1. The computed solutions are shown in Table 5, while the graphical plots are displayed in Figure 5. Though, only the first four components {y1,y2,y3,y4} are shown in the Table of values.
Example 5: HIRES
The High irradiance responses problem consists of a stiff system of 8 nonlinear ordinary differential equation which originates from plant physiology and describes how light is involved in morphogenesis. It explains the high irradiance responses of photo morphogenesis on the basis of phytochrome by means of a chemical reaction involving eight reactants in the form of initial value problem see [28,29].
Table 5. Absolute errors in the numerical integration of example 5
|
x |
Yi |
Radau IIA method [20, 26] |
Method (1.29) |
|
5 |
Y1 |
3.83760043742853 × 10-8 |
5.84532422465145 × 10-11 |
|
Y2 |
2.90659031079721 × 10-8 |
5.86538248525947 × 10-11 |
|
|
Y3 |
2.22044604925031 × 10-16 |
0 |
|
|
Y4 |
0 |
1.11022302462516 × 10-16 |
|
|
50 |
Y1 |
2.32388491339108 × 10-7 |
1.51528067870998 × 10-10 |
|
Y2 |
5.72332533588238 × 10-8 |
3.82774117957396 × 10-10 |
|
|
Y3 |
1.55431223447522 × 10-15 |
3.33066907387547 × 10-16 |
|
|
Y4 |
1.11022302462516 × 10-16 |
4.44089209850063 × 10-16 |
|
|
250 |
Y1 |
1.91869619220464 × 10-8 |
1.42258618079927 × 10-11 |
|
Y2 |
1.09619847643572 × 10-8 |
3.52476554887904 × 10-11 |
|
|
Y3 |
1.38777878078145 × 10-15 |
1.66533453693773 × 10-16 |
|
|
Y4 |
7.77156117237610 × 10-16 |
2.22044604925031 × 10-16 |
|
|
500 |
Y1 |
2.28890865933633 × 10-10 |
2.65111307337423 × 10-13 |
|
Y2 |
1.86748006761241 × 10-10 |
4.33490943878637 × 10-13 |
|
|
Y3 |
3.57353036051222 × 10-16 |
6.93889390390723 × 10-17 |
|
|
Y4 |
4.44089209850063 × 10-16 |
|
a) 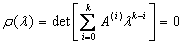 b)
b) 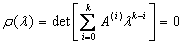
Figure 5. Graphical plots of example 4 using Radau IIA method [20,26] and SDRKC method: a) Solution curve of example 4 using Radau IIA method [20,26], with nfe =500, b) Solution curve of example 4 using method (1.29), with nfe =500
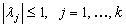
We solve the problem in the interval [0, 1] and compare the graphical plots with the ODE code of Matlab in Figure 6.
a) 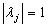 b)
b) 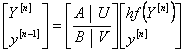
Figure 6. Graphical plots of example 5 using SDRKCM and the ODE code of Matlab: a) Solution curve of example 5 using method (1.25), with nfe = 500, b) Solution curve of example 5 using method (1.29), with nfe = 500
Concluding remarks
In conclusion, the methods so derived in this paper so far have been to introduce a class of implicit second-derivative Runge-Kutta collocation methods suitable for the approximate numerical integration of systems, particularly stiff systems of ordinary differential equations. The derived methods proved an efficient way to find numerical solution to systems of initial value problems when the second derivative terms are cheap to evaluate. We present two new methods of orders four and six that are intended for accurate integration of stiff systems of equations. We have also compared the numerical solution obtained with the conventional Radau Runge-Kutta methods which are widely recognized to be among the most efficient methods for stiff systems [3, 20, 26]. The solution curves are also compared with the exact solutions graphically in Figures.
Acknowledgement
This work was supported by Tertiary Education Trust Fund (TETF) Ref. No. TETF /DAST &D.D/6.13/NOM-CA/BAS&BNAS. Therefore the authors gratefully acknowledged the financial support of the TETF.
The authors are also grateful to the anonymous referee for his/her useful comments and suggestions
References
1. Butcher J. C., Coefficients for study of Runge-Kutta integration processes, J. Austral. Math. Society, 1963, 3(2), p. 185 -201.
2. Enright W. H., Second-derivative multistep methods for stiff ordinary differential equations, SIAM J. Numer. Anal., 1974, 11(2), p. 321-341.
3. Hairer E., Nørsett S. P., Wanner G., Solving Ordinary Differential Equations II: Stiff and Differential Algebraic Problems, Second Revised Edition, Berlin Germany, Springer, 1996.
4. Vigo-Aguiar J., Ramos H., A family of A-stable Runge-Kutta collocation methods of higher order for initial value problems, IMA J. Numer Anal., 2007, 27(4), p.798-817.
5. Cash J. R., High order methods for the numerical integration of ordinary differential equations, Numer. Math., 1978, 30, p. 385-409.
6. Mitsui T., Runge-Kutta type integration formulas including the evaluation of the second derivative, Part I, Publ. RIMS, Kyoto University, Japan, 1982, 18, p. 325-364.
7. Mitsui T., Yakubu D. G., Two-Step Family of Look-Ahead linear multistep methods for ODEs, The science and Engineering Review Doshisha University, Japan, 2011, 52(3), p. 181-188.
8. Urabe M., An implicit one-step method of high-order accuracy for the numerical integration of ordinary differential equations, J. Numer. Math., 1970, 15, p. 151-164.
9. Yakubu D. G., Kwami A. M., Implicit two-derivative Runge-Kutta collocation methods for systems of initial value problems, J. Nigerian Math. Society, 2015, 34, p. 128-142.
10. Dahlquist G., A special stability problem for linear multistep methods, BIT Numer. Math., 1963, 3, p. 27-43.
11. Butcher J. C., Order and stability of Runge-Kutta methods, Nanjing University Conf., 2014.
12. Onumanyi P., Awoyemi D. O., Jator S. N., Sirisena U. W., New linear multistep methods with continuous coefficients for first order initial value problems in ODEs, J. Nigerian Math. Society, 1994, 13, p. 37-51.
13. Lie I., Nørsett S. P., Superconvergence for multistep collocation, Math. Comp., 1989, 52, p. 65-80.
14. Kastlunger K. H., Wanner G., Runge-Kutta processes with multiple nodes, J. Computing, 1972, 9(9), p. 9-24.
15. Chan R. P. K., Tsai A. Y. J., On explicit two- derivative Runge-Kutta methods, Numer. Algor., 2010, 53, p. 171-194.
16. Villadsen J., Michelsen M. L., Solution of Differential Equation Models by Polynomial Approximations, Prentice-Hall, INC, Eaglewood Cliffs, New Jersey, 1978, p. 112.
17. Lambert J. D., Computational Methods in Ordinary Differential Equations, John Willy, and Sons, New York, 1973.
18. Mitsui T., A modified version of Urabe’s implicit single-step method, J. Comp. Appl. Math., 1987, 20, p. 325-332.
19. Burrage K., Butcher J. C., Stability criteria for implicit Runge-Kutta methods, SIAM J. Numer. Anal., 1979, 16, p. 46-57.
20. Butcher J. C., Numerical Methods for Ordinary Differential Equations, 2nd ed. John Wiley & Sons Ltd, 2008, p. 225.
21. Chollom J. P., Jackiewicz Z., Construction of two step Runge-Kutta (TSRK) methods with large regions of absolute stability, J. Comp. and Appl. Maths., 2003, 157, p. 125-137.
22. Butcher J. C., Hojjati G., Second derivative methods with Runge-Kutta stability, Numer. Algor., 2005, 40, p. 415-429.
23. Ali K. E., Hojjati G., Third derivative multistep methods for stiff systems, Intern. J. of Nonlinear Science, 2012, 14(4), p. 443-450.
24. Akinfenwa O. A., Akinnukawe B., Mudasiru S. B., A family of continuous third derivative block methods for solving stiff systems of first order ordinary differential equations, J. Nigerian Math. Society, 2015, 34, p. 160-168.
25. Lambert J. D., Numerical Methods for Ordinary Differential System, John Willy, & Sons, New York, 1991.
26. Butcher J. C., Integration processes based on Radau quadrature formulas, Math. Compt., 1964, 18, p. 233-244.
27. Fatunla S. O., Numerical integrators for stiff and highly oscillatory differential equations, J. Math. Compt., 1980, 34(150), p. 373-390.
28. Gonzalez-Pinto S., Gonzalez-Concepcion C., Montijino J. I., Iterative schemes for Gauss methods, J. Comput. Math. Applic., 1994, 27(7), p. 67–81.
29. Schäfer E., Freiburi Br., A new approach to explain the “High Irradiance Responses” of photomorphogenesis on the basis of phytochrome, J. Math. Bio., 1975, 2, p. 41-56.