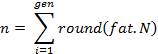A review of the clonal selection algorithm as an optimization method

Ahmed Youssef HATATA, Mohamed Galal OSMAN, and Mohamed  M. ALADL^*

Electrical Engineering Department, Mansoura University, 60 Elgomhoria str., Mansoura City, Egypt

*E-mail: moh.aladl@gmail.com

^* Corresponding author, phone: +201222639922

Abstract

The artificial immune system (AIS) is a new optimization technique which mimics the defence system of animal organisms against pathogens. This paper represents a review of the clonal selection theory (CLONALG), under the roof of AIS. A biological background has been introduced to introduce to the way the CLONALG works in engineering studies. The optimization procedure is presented with a simulation example to illustrates CLONALG optimization process.

Keywords

Artificial Immune System; Clonal Selection Theory; Optimization

Introduction

Natural immune systems (NIS), as the defense system of animal organisms against pathogens, were the inspiration behind the artificial immune systems (AIS). The interest of researchers is generated by such immune system features as: recognition of antigen (AG) characteristics, pattern memorization capabilities, self-organizing memory, adaptation ability, immune response shaping, learning from examples, distributed and parallel data processing, multilayer structure and generalization capability [1].

AIS based algorithms are divided into two major categories: population based and network based. Network based algorithms use the concepts of immune network theory; while population based algorithms use the other theories such as clonal selection and negative selection [2]. This paper puts its focus on the clonal selection theory (CLONALG) as an optimization process. The optimization algorithm starts by defining a purpose function f(x) which needs to be optimized. Some possible candidate solutions are created; antibodies will be used in the purpose function to calculate their affinity and this will determine the ones which will be cloned for the next step. The cloned values are changed, mutated with a predefined ratio and the affinities are recalculated and sorted. After certain evaluations of affinity, affinity with the smallest value is the solution closest to our problem [3].

The CLONALG has some distinguished features. It operates on a population of points in search space simultaneously, not on just one point, does not use the derivatives or any other information, and employs probabilistic transition rules instead of deterministic ones. It also has the ability of getting out local minima. As a relatively novel optimization algorithm, the CLONALG has been successfully applied to solve various engineering problems [4].

Biological background

From Dorland's Illustrated Medical Dictionary [5], the immune system (IS) is a complex system of cellular and molecular components having the primary function of distinguishing self from not self and defense against foreign organisms or substances. So, the main function of the IS that consists of innate and adaptive immunities is to distinguish between foreign molecules that are called antigens (Ag’s) and that constitute self [6]. The innate immunity provides immediate defense of the host and destroys Ag’s using macrophages and natural killer cells. Its immune response has no immunological memory, since the response cannot be alerted by repeated exposure to specific Ag’s. On the other hand, adaptive immunity has an immunological memory for specific Ag’s. The immune response consists of antigen-specific reactions of lymphocytes (T and B cells) which operates as an in-cell mediate and humoral immunities. Each B cell can produce one form of antigen-specific antibodies (Ab’s) to fight with Ag’s [7]. Figure 1, that is adapted from [8], shows an overview of the IS main function.

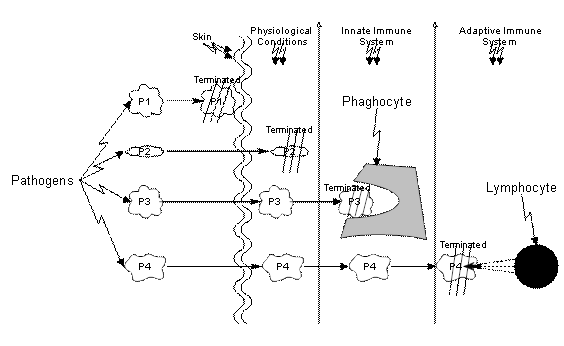
Figure 1. Overview of IS main function [8]

As illustrated in figure 1, if a pathogen attacks the body, the IS defenses will be activated as follows: basic defenses like skin and hair try to block the attacking Ag’s; if the attacking Ag’s passes, it will face physiological conditions like Gastec Juice trying to kill it. The innate immunity will be activated immediately but not specific as a third defense. It uses a phagocyte which is a type of cell within the body capable of engulfing and absorbing bacteria and other small cells and particles (Ag’s). The last line of defense is the adaptive immunity which takes time to be activated but is specific to the attacking Ag’s. Its weapon is the lymphocyte which is a form of small leukocyte (white blood cell) with a single round nucleus, occurring especially in the lymphatic system.

Artificial Immune Systems (AIS)

Many types of algorithm inspired by biological systems, including evolutionary algorithms, swarm intelligence, neural networks and membrane computing [9]. Artificial Immune Systems (AIS) are adaptive systems, inspired by theoretical immunology and observed immune functions, principles and models, which are applied to problem solving [10]. The AIS algorithm is based on three theories: immune network theory, negative selection and clonal selection [2].

Immune network theory

The immune Network theory had been proposed in the mid-seventies. The hypothesis was that the immune system maintains an idiotypic network of interconnected B cells for antigen recognition. These cells both stimulate and suppress each other in certain ways that lead to the stabilization of the network. Two B cells are connected if the affinities they share exceed a certain threshold, and the strength of the connection is directly proportional to the affinity they share [11].

Negative selection

Negative selection is a mechanism employed to help protect the body against self-reactive lymphocytes. Such lymphocytes can occur because the building blocks of Ab’s are different gene segments that are randomly composed and undergo a further somatic hypermutation process. This process can therefore produce lymphocytes which are able to recognize self-Ag’s [9]. The focus of negative selection algorithm is on anomaly detection problems such as computer and network intrusion detection. Besides it is used in time series prediction, image inspection and segmentation, and hardware fault tolerance [2].

Clonal selection principle 

The clonal selection principle is the algorithm used to illustrate how the immune system reacts to Ag’s and its improved capability to eliminate them [11]. Simply, when Ag’s attacks the body, immune cells (B lymphocytes) are responding by producing a specific Ab’s for the attacking Ag’s. Ab’s are molecules attached primarily to the surface of B cells whose aim is to recognize and bind to Ag’s. A proliferation process will occur to the cells that recognized the attacking Ag’s producing two new types: attacking and memory cells. The attacking cells secrete a lot of effective Ab’s to eliminate the attacking Ag’s immediately.  The memory cells have a long-life span in case of future exposures of the same or similar Ag’s, they can act faster and more effectively [12]. The main features of the clonal selection theory are shown in figure 2, that is adapted from [13], and illustrated as follows [8]:

· new cells are cloned of their parents subjected to a mutation mechanism with high rates (somatic hypermutation);

· elimination of newly differentiated lymphocytes carrying self-reactive receptors;

· proliferation and differentiation on contact of mature cells with Ag’s; and

· the persistence of forbidden clones, resistant to early elimination by self-antigens, as the basis of autoimmune diseases.

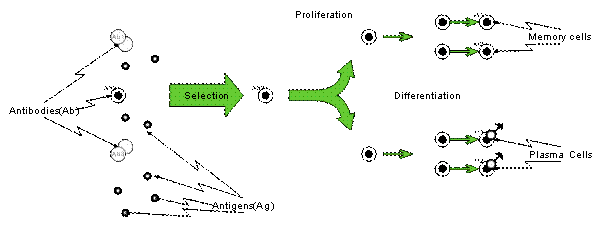
Figure 2. Clonal selection principle [13]

Reinforcement learning and immune memory

Reinforcement learning in the clonal immune system involves cloning the lymphocytes (Ab’s) that are very valuable by better recognizing Ag’s. The Ab’s progeny will be naturally divided into higher affinity that will be cloned temporarily and discarded low affinity Ab’s. It’s very important to ensure an immune response with both high speed and accuracy. The adaptive immune response is stimulated during the initial exposure of the Ag’s. it faces that exposure with a number of B-cells that produces a different affinity Ab’s. During the secondary encounters, the effectiveness of the attacking Ab’s enhanced thanks to the memory cells with the first infection. This is an intrinsic scheme of a reinforcement strategy, where the interaction with the environment gives rise to the continuous improvement of the system capability to perform a given task [14], [15]. Comparing with the primary response facing the first exposure, the second exposure stimulates a secondary response that is characterized by a shorter lag phase, a higher rate and a longer synthesis of Ab’s with high antigenic affinities as shown in figure 3, that is adapted from [14].

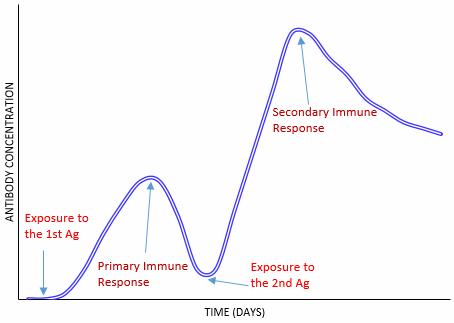
Figure 3. Primary and secondary immune response

Affinity maturation

The repertoire of Ag-activated B-cells in the immune response is divided into: hypermutation and receptor editing. Hypermutation means the affinity of Ab’s increases from a generation to the other thanks to the memory cells that memorize the experience of primary exposure and use that to develop next Ab’s. This process is continuous [14,16]. Random changes of the genes responsible for the Ag-Ab interactions lead to an affinity increase of the Ab. These higher affinity variants are selected to enter the pool of the memory cells. Receptor editing is essential for producing very high affinity Ab’s that can be selected to dominate the response. Cells with low affinity or self-reactive receptors must be efficiently eliminated [17-19].

Optimization

Based on the biological concept of AIS, optimization techniques have been built considering AIS theories: immune network theory, negative selection and clonal selection. This paper focuses on the clonal selection optimization algorithm (COLNALG). But, at first it should be noted that [14]:

· instead of antigen population, there is an objective function to be optimized;

· each antibody Ab represents an element of the input space;

· Ab’s affinity corresponds to the evaluation of the objective function for the given Ab;

· number of clones generated n, for  Ab’s will be

(1)

where n is the total number of clones generated for each of the Ag’s, f at is a multiplying factor, N is the total number of Ab’s, gen is the number of iterations and round is the operator that rounds its argument toward the closest integer. Each term of this sum corresponds to the clone size of each selected Ab. For N=100 and f at=1 each affinity antibody Ab (i=1) will produce 100 clones.

Material and method

Proposed CLONALG procedure

In the proposed CLONALG algorithm which was originally proposed by De Castro and Van Zuben [20], feasible and infeasible Ab’s are distinguished and sorted due to their fitness and constrained violation values, respectively [14]. This process is a part of the algorithm procedure as follows:

1. Generate a set of random antibodies which are the current candidate solutions of the objective function.

2. Calculate the affinity values of each candidate solutions by calculating the objective function using each candidate.

3. Sort the antibodies starting from the lowest affinity.

4. Clone the better matching antibodies more with some predefined ratio.

5. Mutate the antibodies with some predefined ratio. This ratio is obtained in a way that better matching clones mutated less and weakly matching clones mutated much more in order to reach the optimal solution.

6. Calculate the new affinity values of each antibody.

7. Repeat Steps 3 through 6 while the minimum error criterion is not met

Figure 4 shows the flowchart of the CLONALG procedure.

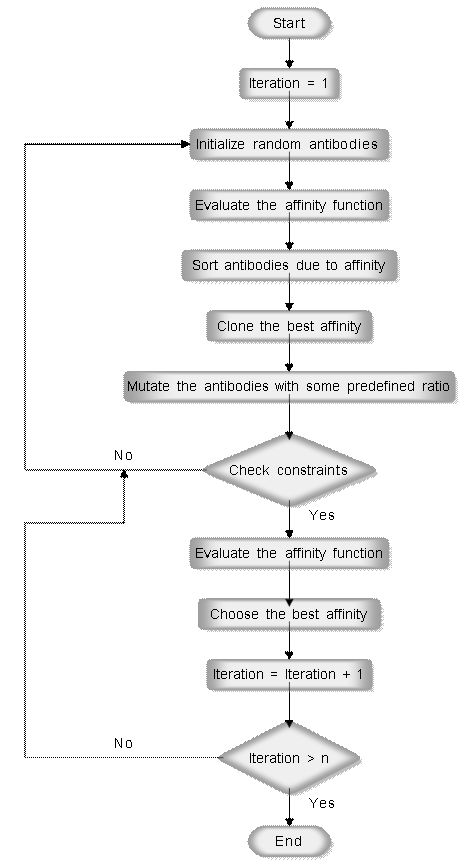
Figure 4. A flowchart of the CLONALG procedure

Simulation

To illustrate the CLONALG optimization technique, consider the objective function f(x,y) which is intended to be optimized:

(2)

where f(x,y) is the objective function to be optimized and x&y are the corresponding antibodies.

The purpose is to find the maximum value of the objective function and the corresponding values of the antibodies x and y which are defined over the range [-1,1]. The running parameters according to (1) are: N=100, f at=0.1 and gen=25. The main steps of the proposed technique are as follows:

Step 1.  Generate random values of the antibodies  x and y producing an initial search space of 100 populations as shown in figure 5;

Step 2.  Evaluate the objective function f(x,y) corresponding to step 1;

Step 3.  Sort the new values of the objective function f(x,y) in ascending order;

Step 4.  Sort the corresponding values of the antibodies x and y in the corresponding order of the objective function f(x,y);

Step 5. The best individuals are reproduced (cloned) by the following function;

% Reproduction

function [T,pcs] = reprod(n,fat,N,ind,P,T);

% n   -> number of clones

% fat -> multiplying factor

% ind -> best individuals

% T   -> temporary population

% pcs -> final position of each clone

if n == 1,

cs = N;

T = ones(N,1) * P(ind(1),:);

else,

for i=1:n,

% cs(i) = round(fat*N/i);

cs(i) = round(fat*N);

pcs(i) = sum(cs);

T = [T; ones(cs(i),1) * P(ind(end-i+1),:)];

end;

end;

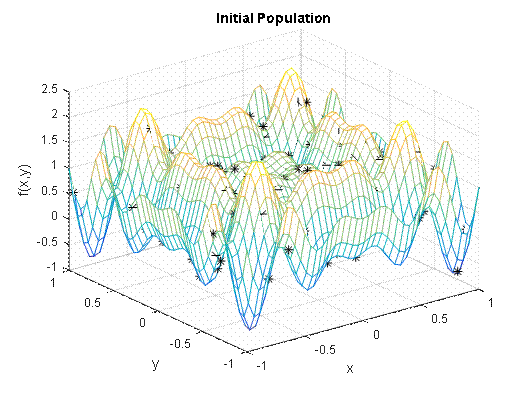
Figure 5. Initial search space

Step 6. Mutate the antibodies with a mutation probability P_m=0.01. Figure 6 shows the antibodies population after the cloning and mutation processes;

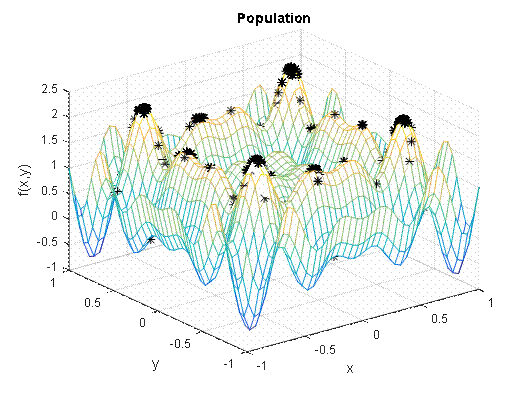
Figure 6. Antibodies population after the cloning and mutation processes

Step 7.  The affinity of the antibodies  and  will be calculated again;

Step 8. Steps will be repeated according to number of iterations.

Results and discussion

Table 1 shows the best optimization result for each iteration.

As illustrated in Table 1 and Figure 7, the optimal results found f(x,y)=2.26 that is at values x=-0.63 and y=0.63.

Table 1. Optimization results

Iteration	x	y	f(x,y)
1	-0.65	0.55	1.930
2	-0.65	0.55	1.943
3	-0.65	0.61	2.227
4	-0.65	0.61	2.229
5	-0.65	0.65	2.230
6	-0.64	0.65	2.251
7	-0.64	0.65	2.251
8	-0.64	0.65	2.251
9	-0.62	-0.64	2.253
10	-0.63	0.62	2.254
11	-0.64	0.63	2.260
12	-0.64	0.63	2.260
13	-0.64	0.63	2.260
14	-0.64	0.63	2.260
15	-0.64	0.63	2.260
16	-0.64	0.63	2.260
17	-0.64	0.63	2.260
18	-0.64	0.63	2.260
19	-0.64	0.63	2.260
20	-0.64	0.63	2.260
21	-0.63	0.63	2.260
22	-0.63	0.63	2.260
23	-0.63	0.63	2.260
24	-0.63	0.63	2.260
25	-0.63	0.63	2.260

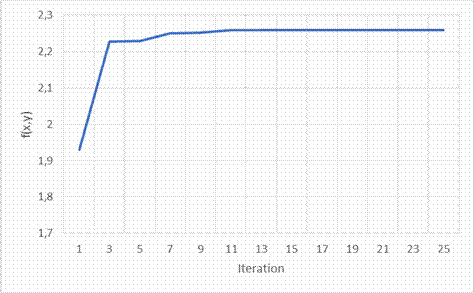
Figure 7. Objective function values

It should be noted that CLONALG optimization method is capable of providing more accuracy with each iteration processed. Thanks to its memorization capability that memorize the experience of primary solution and use adaptation ability to develop the next one. As shown in Figure 7, the solution of the optimization process is being improved with every iteration processed, until reaching the best results found.

To sum-up, this paper reviewed the three theories of artificial immune systems (AIS): immune network theory, negative selection and clonal selection (CLONALG). Focusing on the CLONALG verified that it’s capable of performing learning and maintenance of high quality memory and solving complex problems. Simulation results confirm its effective and efficient ability in solving the tested problem. This optimization code can be modified for solving various engineering optimization problems. In a future work, the CLONALG code is modified to get the optimum size of a hybrid power system consists of PV Panels, Wind Turbines and Batteries. The objective function is considered as the cost function of the hybrid system and the antibodies are considered as the components of the hybrid system. The main goal of the optimization process is to satisfy the hourly load demand with the least probability of cut-off power and the minimum overall cost.

References

1. Dudek G., An artificial immune system for classification with local feature selection, IEEE Transactions on Evolutionary Computation, 2012, 16(6), p. 847-60.

2. Zheng J., Chen Y., Zhang W., A Survey of artificial immune applications, Artificial Intelligence Review, 2010, 34(1), p. 19-34.

3. Ulker E. D., Ulker S., Comparison study for clonal selection algorithm and genetic algorithm, arXiv preprint arXiv:1209.2717. 2012 Sep 12.

4. Babayigit B., Guney K., Akdagli A., A clonal selection algorithm for array pattern nulling by controlling the positions of selected elements, Progress In Electromagnetics Research B, 2008, 6, 257-66.

5. Combs D., Dorland's Illustrated Medical Dictionary, Journal of Family Practice, 1995.

6. Farmer J. D., Packard N. H., Perelson A.S., The immune system adaptation and machine learning, Physica D: Nonlinear Phenomena, 1986, 22(1), p. 187-204.

7. Wu J.Y., Artificial immune system for solving constrained global optimization problems, IEEE Symposium on Artificial Life, 2007, pp. 92-99.

8. De Castro L. N., Von Zuben F. J., Artificial immune systems: Part I–basic theory and applications, Universidade Estadual de Campinas, Dezembro de, Tech. Rep. 1999, 210.

9. Timmis J., Hone A., Stibor T., Clark E., Theoretical advances in artificial immune systems, Theoretical Computer Science, 2008, 403(1), p. 11-32.

10. De Castro L.N., Timmis J., Artificial immune systems: a new computational intelligence approach, Springer Science & Business Media, 2002.

11. Aickelin U., Dasgupta D., Gu F., Artificial immune systems, InSearch Methodologies, 2014, pp. 187-211.

12. De Castro L. N., Timmis J., An artificial immune network for multimodal function optimization, Evolutionary Computation, 2002. CEC'02. Proceedings of the 2002 Congress, 2002, 1, p. 699-704.

13. De Castro L. N., Von Zuben F. J., de Deus Jr. G. A., The construction of a Boolean competitive neural network using ideas from immunology, Neurocomputing, 2003, 50, p. 51-85.

14. De Castro L. N., Von Zuben F. J., Learning and optimization using the clonal selection principle, IEEE Transactions on Evolutionary Computation, 2002, 6(3), p. 239-51.

15. Sutton R. S., Barto A.G., Reinforcement learning: An introduction, Cambridge: MIT press, 1998.

16. Banerjee S., An Immune System Inspired Approach to Automated Program Verification, arXiv preprint arXiv:0905.2649. 2009 May 16.

17. Berek C., Ziegner M., The maturation of the immune response, Immunology Today, 1993, 14(8), p. 400-4.

18. George A. J., Gray D., Receptor editing during affinity maturation, Immunology Today 1999, 20(4), 196.

19. Nussenzweig M. C., Immune receptor editing: revise and select, Cell, 1998, 95(7), 875-8.

20. De Castro L.N., Von Zuben F.J., The clonal selection algorithm with engineering applications, Proceedings of GECCO, 2000, 2000, pp. 36-39.