Mathematical description of resources distribution for logistics information systems
Safwan AL SALAIMEH
Software Engineering Department, Aqaba University of Technology, Fifth Zone, Building Block 84, Aqaba, Jordan
E-mails: ssalaimeh@aut.edu.jo
Abstract
The methodology of resources allocation and the mathematical description of the problem are presented. The problem is founded in the class of linear programming models and the modified simplex method to find optimal solutions is designed. An example is given to illustrate the implementation of the developed methodology.
Keywords
Logistics; Linear programming; computerized system; Mathematical model; Resource distribution; linear programming
Introduction
Logistics is a science of planning, monitoring, transportation management and storing of finished products and raw materials starting from the buyer and ending with the consumer not to mention the transfer, saving and process of data. The technological logistics system is considered as support for these systems, in terms of information and computerized discipline [1-3].
The concepts of logistics system are focused on cooperative logistics concepts like Supply Chain Management [2], Efficient Consumer Response (ECR) or Quick Response (QR). Ni Wang, Jye-Chyi Lu and Paul Kva declared that these concepts are actually discussed in recent logistics publications, were typical descriptions of temporary logistics systems are characterized by notions of push/pull control logic, postponement/decentralization of stock keeping as alternative or complementary strategic opportunities for the design of logistics networks [4-6].
The process of building logistic information system that can be practically used to solve applied economic problems goes through the following phases [7-, 8, 9]:
1. To collect the data needed for the use of logistic information systems.
2. To design a mathematical model suitable for the use of logistic information systems.
3. To design a simulation system, introduce applications and achieve the required results.
4. Users interfaces.
Problem of resource distribution for logistics information systems
Between 10% and 13% of a rich country’s gross domestic product (GDP) can be credited to logistics-related costs for the movement of parts, components and finished goods between suppliers, manufacturers, and customers [10,11,12]. Today’s globally detached supply chains make having access to logistics data business imperatives.
Bayarov mentioned in his article that a distributed control system is made up of interacting component objects, each of which have persistent local state and one or more threads of control which may come from feedback [13-15]. Other input messages may come in an uncontrolled fashion from the system's environment. Output messages called observations can be routed as feedback to other objects [16, 17]. Any communication can experience arbitrary delay.
Theoretically, a simple specification of a distributed control system consists of the descriptions of several components: state, computation, uncontrollable variables, and constraints (including an objective function).
The state of a distributed system is described in terms of its components. In our context, the components are the system's participating objects, as well as the communication infrastructure itself. The objects can be constant, can communicate with other objects, and can have one or more local threads of control. Each object has access to its own local state. However, no object can openly access the local states of other objects, nor can it directly access the state of the distributed system itself [18, 19].
If a resource to understand everything that is used in the production and business (people, finances, time, goods, energy), it can be argued that the most important task of planning and management is the allocation of resources. The classical problem of their distribution is reduced to ensure that the resources available to distribute the work to be performed If resources were sufficient for effective (quality, timely, cheap) performance of all work, then the task would not have arisen. In a real situation, there are always shortages of some resources. Moving from one mechanism to implement others leads to a change in the overall effectiveness of the implementation of all works together, this implies that it is desirable to distribute the available resources in such a way that maximizes the total revenue (profit) enterprises or the minimum total cost (the cost) [20].
Effective planning of enterprises based on the assumption of legitimate constraints of available resources, without which it would lose its meaning to compare different versions of the planning decisions. The optimum planning of any scarce resource, in contrast to non-deficient fully utilized, but if the amount changes, changing, and the optimal objective function value. If you change the scarce resource is changed and the optimal objective function value. Changing the resource may have a deterministic nature (explicitly depend on time) have a stochastic character (onset of the epidemic in a given season can be predicted with a given probability), or be uncertain, depending on various factors.
The description of resources distribution
The problem of distribution resources arises whenever the planning of the operation, when the resources available to carry out all work the best is not enough. By their functional problems of resource allocation can be divided into three groups:
1) Allocate resources given between scheduled to perform work in such a way as to maximize profit or minimize the expected cost [17].
2) Determine the resources needed to execute the works in order to minimize the total costs of production [18].
3) Determine the scope of work that can be done given resources [19]. At the optimum distribution resources, various modifications of the classical problems of linear, nonlinear and integer mathematical programming in bad and good conditions for systems of functional limitations in deterministic and stochastic fuzzy statements. The problem of optimal distribution resources is reduced to make the most efficient way to distribute the given scarce resources, ensuring the maximum possible output of commodities, while optimizing a selected criterion of efficiency (amount of output, income, costs, capital expenditures, profitability, etc.) [13-15].
If the optimality criterion to choose the total profit of the company F(x), then the objective function in the linear approximation can be represented by the expression in Eq(1).
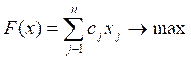 (1)
(1)
where cj = Profit of product and xj = Product type.
Restrictions are imposed on the variables of the model dedicated resources to fund the time of the equipment or available financial resources in the form of relations:
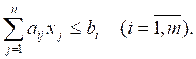 (2)
(2)
The no negativity of the variables is written in the form of constraints:
![]() (3)
(3)
Mathematical model (1)-(3) applies to the simplest type of resource allocation models in the class of linear programming problems. In general, the model (1) - (3) may include limitations on hardware resources bi, in the form of time fund of the ith group of equipment:
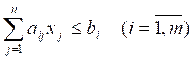
restrictions on the variables of assortment products xj as ranges from every variables
![]()
![]()
constraints on consumption materials, labor costs and payroll.
The real problem of distribution resources are reduced
to finding a value of the vector variables ![]() which delivers
extreme (for a given maximum) to one or more particular criteria
which delivers
extreme (for a given maximum) to one or more particular criteria ![]() ,
keeping the others
,
keeping the others ![]() at some level
at some level ![]() :
:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Solution of (4) - (6) shall be given set of constraints. Functional limitations (5) reflect the analytical dependence of the type of balance equations and the statistical dependence of the type of production functions. Part of the role of functional limitations criterion constraints
![]() (7)
(7)
Under which the quasi-optimal version of the plan is implemented parameters of functional limitations are determined by the results of observations, so they contain various kinds of uncertainty. The main reasons for their occurrence are hard-stabilized modes of operation of manufacturing processes, changing non-random manner and conditions of the manifestation of the environment, unpredictable volitional organizational issues, changing the effect of aging and wear equipment. In models of optimal distribution resources uncertainty is manifested in the uncertainty and incompleteness of initial data bad conditions of functional limitations, inadequacies and contradictions of the relations used by the system constraints. In multi objective problems, it is determined original data regularization for estimating the parameters of functional limitations, approximating ill-posed problem with stretching and convolution of partial criteria.
By varying the model parameters over a range of task allocation in a class of linear programming
![]() (8)
(8)
Replacement of a parametric programming problem, which is close to the original:
![]() (9)
(9)
where ![]() - perturbed parameter
values
- perturbed parameter
values ![]() in some metric such as Euclidean:
in some metric such as Euclidean:
![]() (10)
(10)
Below investigate the parameters relative to the deviation of specific types of resources from their nominal values.
The solution
Below is a selection method of optimal solutions of the problem of resources allocation that are resistant to deflection of the initial parameters established on the basis of the classic table and the dual simplex method, a method of analysis of the compatibility of functional limitations and the method of regularization of ill-conditioned system functional limitations. Computational scheme of the method shown in the figure consists of five main blocks: 1, 4, 5, 8, 9. assignment of blocks of the computational scheme is illustrated in the process of solving the problem of distribution resources to a specific example. Supposing that we have a company that produces four types of products TP1 - TP4 using three types of resources, standards and standards flow are received from the sale of revenue are shown in Table 1. Financial, labor, and raw material are listed as distribution of resource types among four types of products to determine the production costs as well as production plan by maximization the profit.
Table 1. Baseline data of the distribution resources
|
Types of used resource |
Types of products |
Disposable resource |
|||
|
TP1 |
TP2 |
TP3 |
TP4 |
||
|
Financial |
1 |
1 |
1 |
1 |
16 |
|
Labors |
6 |
5 |
4 |
3 |
110 |
|
Raw materials |
4 |
6 |
10 |
13 |
100 |
|
Profit per unit of production plan |
60 |
70 |
120 |
130 |
---- |
|
Plan |
X1 |
X2 |
X3 |
X4 |
---- |
In constructing a mathematical model distribution volume of production is denoted by xj, and the profit per unit of product through cj production costs are determined by the following resources. Financial a1j, j=1,2,…,n, labor a1j = 1,2,…,n and raw material a3j, j=1,2,…,n. Results have the following: financial resources b1, labor b2, material and natural resources b3. Linear mathematical model of distribution resources is formally written as follows:
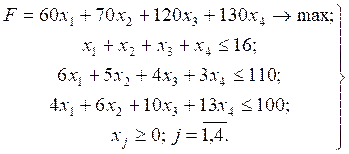
In this system table simplex method derived optimum production plan by product line x1* = 10, x2* = 0, x3* = 4, x4* = 0 with the amount of profit made F=1320, and the reserves of raw materials resources was 26 units, indicating that its surplus. There are a number of natural questions: whether there will be a solution to be optimal if the relative decline in profit contribution of one of the variables in the model, what effect a reduction of, which happens to the optimum, if you enter into a new managed model variable. The above problems are solved by the methods of analyzing the stability of decisions rejecting distributed resources. At the same time interest is the situation: what happens in the enterprise, if: a) 6 out of 16 workers to divert to other works, and b) the supply of resources to reduce by 20%, c) the performance of equipment to increase by 50%, and how it affects the output. In other words, it is desirable to know the area of optimal solutions that are resistant to deviations of resource constraints.
It is known that each original linear programming problem corresponds to a certain dual problem. Its variable, called the dual variable to evaluate the influence of changes in each type of resource for objective function (in connection with this dual variable are often referred to as the dual of the assessment, important that in order to find dual assessments are not required to solve the dual problem). The values of the dual assessments already been obtained by simplex table optimal solution of initial task. Learn the value of the dual estimates can be as follows. If an ith resource is not fully used, then an additional variable in the limit for this resource is greater than zero. In the analyzed example of such a resource supports raw b2 = 110, and its reserve y2 = 26 (if the raw material was not 110, but 112, the reserve equal 26, but 28, thus increase the objective function would not have happened).
Thus, if a particular resource on a reserve, the additional variable is the base, and its dual score is zero. In our example, labor and equipment used in full, so they are more variables are zero. If the resource is fully utilized, then the change (increase or decrease) will affect the volume of production and, ultimately, the objective function: it will increase or decrease the size of its own estimates. The values of additional variables and dual estimates indicate that at growth of labor per unit of the objective function increases by 20 pcs, reaching a value of F = 1340, a reduction in their unit obtain F = 1300. Growth per unit of equipment will increase the objective function at 10 units, t. e. gets F = 1330, and in its reduction by one F = 1310.
The methodology of distribution resources and the mathematical description of the problem clouded in the class of linear programming models, the modified simplex method to find optimal solutions, are designed in this paper and given a concrete example to illustrate the implementation of the developed methodology.
The results gained by using method of optimal solutions of the resources allocation that are resistant to deflection of the initial parameters established on the basis of the classic table and the dual simplex method. The results show that a maximization profit per unit of production plan
Based on above mentioned problem of distribution resources and models of logistic information systems, we can say that it was a matter of accurate modeling for them the ideal distribution, taking into account the error value for all parameters, where we found that the error is very small so as not to affect the final result, as shown in Equation (10).
Conclusion
Our results gained by using method of optimal solutions of the resources allocation that are resistant to deflection of the initial parameters established on the basis of the classic table and the dual simplex method. The results show that a maximization profit per unit of production plan
References
1. Al Salaimeh S., The Optimal Management of Information Servicing Logistics System, Institute Mathematics and Computer Science Journal, 2003, India.
2. Wang N., Lu J. C., Kvam P., Reliability modeling in spatially distributed logistics systems, IEEE Transactions on Reliability, 2006, 55(3), p. 525-534.
3. Al Salaimeh S., Information Technologies of Distributed Applications Design, Institute Mathematics and Computer Science Journal, 2003, p. 99-103.
4. Bayarov S., Resource functions for model based performance analysis of distributed software systems, Carleton University, 1999.
5. Al Salaimeh S., Makadmeh Z., Multi-Criteria Synthesis of Logistics Systems Through the Hierarchy Analysis, Journal of Cybernetics and Informatics. 2006; 6, p. 15-25.
6. Al Salaimeh S., Batiha K., Business Process Simulation with Algebra Event Regular Expression, Information Technology Journal, 2006, 5(3), 583-589.
7. Batiha K., Al Salaimeh S., E-Learning, Leonardo Electronic Journal of Practices and Technology, 2006, 5(9), p. 1-4.
8. Batiha K., Al Salaimeh S., Al Besoul K., Digital Art and Design, Leonardo Journal of Science, 2006, 5(9), p. 1-8.
9. Al Besoul K., Al Salaimeh S., The Structure of logistics organizational technological system, Journal Information Society, 2007, 4(7), p. 40-45.
10. Bandy H., Modeling Trading System Performance, Blue Owl Press, 2011.
11. Yan H., Yin G., Zhang Q, Stochastic Processes, Optimization, and Control Theory: Applications in Financial Engineering, Queuing Networks, and Manufacturing Systems, Springer, USA, 2006.
12. Guernsey G. Y., Process Dynamics: Modeling, Analysis, and Simulation, Prentice Hall, United Kingdom, 2003.
13. Bretscher O., Linear Algebra with Applications, Prentice Hall, UK, 2008.
14. Akuna S. T., Software processing modeling, Springer, USA, 2005.
15. Bidgoli H., Modern Information Systems for Managers, Academic Press, 2009.
16. Daganzo C. F., Logistics Systems Analysis, Springer; 2010.
17. Shridhara Bhat K., Text Book of Production Management, Students Edition, Himalaya, USA, 2002.
18. Gerasimos Rigatos, Intelligent Industrial Systems: Modeling, Automation and Adaptive Behavior (Premier Reference [4] Source), Information Science Reference; First edition (April 1, 2010).
19. Kersting W. H., Distribution System Modeling and Analysis, CRC Press, 2001.
20. Jeanblanc M., Yor M., Chesney M., Mathematical Methods for Financial Markets, Springer; 1st Edition, 2009.