Comparison of Euler and Range-Kutta methods in solving ordinary differential equations of order two and four
David I. LANLEGE1*, Rotimi KEHINDE1, Dolapo A. SOBANKE1, Abdulrahman ABDULGANIYU2, and Umar M. GARBA2
1Department of Mathematical Science, Federal University Lokoja P.M.B 115 Lokoja Kogi State, Nigeria.
2 Department of Mathematics/Computer Science, Ibrahim Badamasi Babangida University Lapai P.M.B 11 Lapai Niger State, Nigeria.
E-mail(s): loislanlege@yahoo.com (DIL); kennyrot2000@yahoo.com (REK); garbaumar49@yahoo.com (UMG)
* Corresponding author, phone: +2348030528667, +2348131235684
Abstract
The purpose of this to produce efficient numerical methods with the same order of accuracy as that of the main starting values for exact solutions of fourth order differential equation without reducing it to a system of first order differential equations. The methods of the differential systems arising from the approximate solution to the problem are adopted using the Runge-Kutta method and stages. The methods were compared and contrasted based on the results obtained. †The comparison shows that Euler method gives accurate approximate result than Runge-Kutta method. After the derivation of the formulae of O(h2), the comparison was done in regards to identify the formula with higher accuracy.
Keywords
Numerical Analysis; Numerical Approximation; Exact Solution; Accuracy; Runge-Kutta and Euler
Introduction
Numerical analysis is a branch of mathematics that deals with the study of methods and procedures used to obtain approximate solutions to mathematical problems. EndreSull and David Mayer defined the numerical analysis as †a branch of mathematics that provides the theoretical foundation for the numerical algorithm we rely on to solve a multitude of computational problem in mathematical models or the study of algorithms that use numerical approximation (as opposed to general symbolic manipulations) for the problems of mathematical analysis [1]. Numerical analysis naturally finds applications in all fields of engineering and the physical science, but in this 21st century, the life science and even the arts have adopted elements of scientific computations [2].
The overall goals of the field of numerical analysis in the design and analysis of techniques to give approximate but accurate solution are hard to get. It is therefore, important to be able to estimate the error involved in such approximation. Thus, the aims of this work was to compare between Euler and Runge-Kutta methods to a rigorous analysis in order to demonstrate the efficiency of the methods to other similar techniques. It was also examine the effect of the steps on the accuracy of the techniques.
Eulerís method is more preferable than Runge-Kutta method because it provides slightly better results. Its major disadvantage is the possibility of having several iterations that result from a round-error in a successive step.
Secularity band differences in the results of some numerical methods with the standard Eulerís method of order three and four was examined.
Material and method
Euler method
In mathematics and computational science, the Euler method is a first-order numerical procedure for solving ordinary differential equation (ODEs) with a given initial value. It is the most basic explicit method of numerical integration of ordinary differential equation and is the simplest Runge-Kutta method. The Euler method is named after Leonhard Euler (1707) [3].
Two approaches named standard Euler method and modified Euler method are known.
Standard Euler method
The standard Eular method which is the first order Runge-Kutta method was derive by Leonarhd Euler (1707-1783) [4].
Consider the initial value problem, the first order
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (1)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (1)
where ![]() †is
the first order differential equation;
†is
the first order differential equation; ![]() †is the function of x
and y;
†is the function of x
and y; ![]() is the solution to the
differential equation in equation (1) at
is the solution to the
differential equation in equation (1) at ![]() †given as
†given as ![]() ;
;
![]() †is
the value of y obtained at
†is
the value of y obtained at ![]() and
and ![]() is the point
for which y is obtained as
is the point
for which y is obtained as ![]()
![]() ††††††††††††††††††††††††††††††††††††††††† ††††††††††† (2)
††††††††††††††††††††††††††††††††††††††††† ††††††††††† (2)
Thus,
![]() †††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (3)
†††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (3)
†![]() † ††††††††††† ††††††††††† (4)
† ††††††††††† ††††††††††† (4)
Let ![]()
![]() ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† (5)
††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† (5)
equation (5) is the same as
![]() ††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (6)
††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (6)
![]() †††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† (7)
†††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† (7)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (8a)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (8a)
![]() ††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (8b)
††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (8b)
Equation (8b) is known as standard Euler method.
Modified Euler method
This method is a second order Runge-Kutta [5]. The convergence in this method is higher due to a higher degree of accuracy as compared to the standard Euler.
![]() ††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (9)
††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (9)
DERIVATION:
Considering the Taylors series of ![]() †about h given
by
†about h given
by
![]() †††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (10)
†††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (10)
Truncating when ![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (11)
††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (11)
From the definition of derivatives
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (12)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (12)
![]() †††††††††† ††††††††††††††††††††††† (13)
†††††††††† ††††††††††††††††††††††† (13)
Thus,
![]() ††††††††††††† ††††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (14)
††††††††††††† ††††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (14)
![]() †††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (15)
†††††††††† ††††††††††† ††††††††††† ††††††††††††††††††††††† (15)
Substitute ![]() †and
†and
![]() into
equation (6):
into
equation (6):
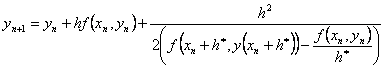 ††††††††††† ††††††††††††††††††††††† (16)
††††††††††† ††††††††††††††††††††††† (16)
Let
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (17)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (17)
Then we have
![]() †††††††††††††††† ††††††††††††††††††††††† (18)
†††††††††††††††† ††††††††††††††††††††††† (18)
![]() †††††††††††††††††††††††† ††††††††††† (19)
†††††††††††††††††††††††† ††††††††††† (19)
![]() †††††† ††††††††††† (20)
†††††† ††††††††††† (20)
![]() ††††††† ††††††††††† (21)
††††††† ††††††††††† (21)
![]() ††††††††††††††††† ††††††††††† (22)
††††††††††††††††† ††††††††††† (22)
Equation (22) can be written as
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (23)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (23)
where
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (24)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (24)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (25)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (25)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (26)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (26)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (27)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (27)
Let
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (28)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (28)
 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (29)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (29)
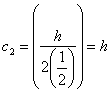 ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (30)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (30)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (31)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (31)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (32)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (32)
Hence,
![]() †††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (34)
†††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (34)
OR
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (35)
††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (35)
Runge-Kutta method
The Runge-Kutta method is also a second order Runge-Kutta Method using Taylors series expansion to derive it, like modified Eulerís method [6].
From equation (22)
![]() †††††††††† ††††††††††† (36)
†††††††††† ††††††††††† (36)
Equation (36) can be written as
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (37)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (37)
where:
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (38)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (38)
![]() †††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (39)
†††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (39)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (40)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (40)
![]() ††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (41)
††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (41)
Let
![]() † ††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (42)
† ††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (42)
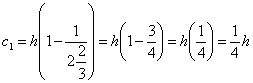 †††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (43)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (43)
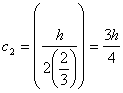 †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (44)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (44)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (45)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (45)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (46)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (46)
![]() †††††††††††††††††† ††††††††††† ††††††††††† (47)
†††††††††††††††††† ††††††††††† ††††††††††† (47)
![]() † ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (48)
† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (48)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (49)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (49)
Third-stage Runge-Kutta method
The third-stage Runge-Kutta method express how formulations of k iterations are obtained.
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (50)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (50)
where
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (51)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (51)
![]() ††††††††††††††††††††††††††††††††††††† ††††††††††† (52)
††††††††††††††††††††††††††††††††††††† ††††††††††† (52)
Equation (52) is the third order Runge-Kutta method with error of† order h4.
Fourth-stage Runge-Kutta
One of the most frequently used of the Rung-Kutta family is the fourth order Runge-Kutta method or the classical fourth order Runge-Kutta method [7]. This method is generally superior to second order, its derivative is algebraically complicated and involves five equations.
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (53)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (53)
where:
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (54)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (54)
![]() ††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† (55)
††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† (55)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (56)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (56)
Other renowned mathematicians that worked on this method are Runge-Kutta-Fehlberg and Runge-Kutta Nystrom.
Fehlbergís fifth Ė order Rk †methodis:
![]() †††††††††††† ††††††††††††††††††††††† ††††††††††† (57)
†††††††††††† ††††††††††††††††††††††† ††††††††††† (57)
where:
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (58)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (58)
![]() ††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (59)
††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (59)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (60)
††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (60)
![]() †††††††††††††††††††††††††† ††††††††††† (61)
†††††††††††††††††††††††††† ††††††††††† (61)
![]() †††††††††††† ††††††††††††††††††††††† (62)
†††††††††††† ††††††††††††††††††††††† (62)
![]() ††††††††††††††††††††† (63)
††††††††††††††††††††† (63)
A Finnish mathemathecian E.J. Nystron derived his own formular using the Runge-Kutta method [8].
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (64)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (64)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (65)
††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (65)
![]() †††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (66)
†††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (66)
![]() ††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (67)
††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (67)
![]() ††††††††††††††††††††††††††††† ††††††††††† (68)
††††††††††††††††††††††††††††† ††††††††††† (68)
![]() ††††††††††††††††††††††††††††††† ††††††††††† (69)
††††††††††††††††††††††††††††††† ††††††††††† (69)
Implementation of Euler method and Runge-Kutta method
The Euler and Runge-Kutta methods as previously deduced was used in this study to solve differential equations.
Standard Euler method
From equation (8), we have the formula
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (70)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††† (70)
Consider the differential equations in equations (71 and 86) of the initial value problem below:
![]() †††††††††††††††††† ††††††††††† (71)
†††††††††††††††††† ††††††††††† (71)
Solution:
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (72)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (72)
where
![]() †††††††††††††††††††††††††††††††††††† ††††††††††† (73)
†††††††††††††††††††††††††††††††††††† ††††††††††† (73)
when ![]()
![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (74)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (74)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (75)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (75)
when ![]()
![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (76)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (76)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (77)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (77)
when ![]()
![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (78)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (78)
![]()
![]() †††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (79)
†††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (79)
![]() †††† ††††††††††† (80)
†††† ††††††††††† (80)
![]() †††††††††††††††††† (81)
†††††††††††††††††† (81)
Numerical illustration of exact solution for Example 1
The example below in equation (82) illustrates the application of exact solution for the solution of differential equations
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (82)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (82)
If ![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (83)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (83)
when ![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (84)
†††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (84)
when ![]()
![]() †† ††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (85)
†† ††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (85)
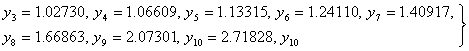 †† ††††††††††† (86)
†† ††††††††††† (86)
Consider the differential equation of the initial value problem:
![]() †††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††† (87)
†††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††† (87)
Exact solution
![]() † ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (88)
† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (88)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (89)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (89)
where
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (90)
†††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† (90)
when ![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††††††††††††††††
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (91)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (91)
when ![]()
![]()
![]() †††††††††††††††††††††††††† ††††††††††† (92)
†††††††††††††††††††††††††† ††††††††††† (92)
when ![]()
![]() ††††††††††††††††††††††††††††††††
††††††††††††††††††††††††††††††††
![]() ††††††††††††††††††††††††† ††††††††††† (93)
††††††††††††††††††††††††† ††††††††††† (93)
![]() ††††††††††††††††††††††††† ††††††††††† (94)
††††††††††††††††††††††††† ††††††††††† (94)
![]() ††††††††††††††††††††††††††† ††††††††††† (95)
††††††††††††††††††††††††††† ††††††††††† (95)
![]() ††††††††††††† ††††††††††† ††††††††††† (96)
††††††††††††† ††††††††††† ††††††††††† (96)
Numerical illustration of exact solution for Example 2
Example 2 below in equation (97) is solved by finding the† exact solution† for the solution of differential equations
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††† (97)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††† (97)
![]() †††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††† (98)
†††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††† ††††††††††† (98)
when ![]()
![]() †††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (99)
†††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (99)
when ![]()
![]() ††††††††††††† ††††††††††† (100)
††††††††††††† ††††††††††† (100)
when ![]()
![]() ††††††††††††††† (101)
††††††††††††††† (101)
![]() ††††††††††††††††††††††††††† (102)
††††††††††††††††††††††††††† (102)
![]() †††† ††††††††††† ††††††††††† (103)
†††† ††††††††††† ††††††††††† (103)
Modified Euler method
This is the second Eulerís method we are considering as deduced in equations (23-35) and expressed as:
![]() †††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (104)
†††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (104)
where
![]() †††††††††††††††††††††††††††††††† ††††††††††† (105)
†††††††††††††††††††††††††††††††† ††††††††††† (105)
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (106)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (106)
Let us consider the same differential equations in equations (72 and 87):
![]() †††††† ††††††††††† (107)
†††††† ††††††††††† (107)
Solution
![]() ††† ††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (108)
††† ††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (108)
when ![]()
![]()
![]()
![]() †
†
†![]() †††††††††† ††††††††††† (109)
†††††††††† ††††††††††† (109)
when ![]()
![]()
when ![]()
![]()
![]()
![]() ††††††††††††† ††††††††††† ††††††††††† (110)
††††††††††††† ††††††††††† ††††††††††† (110)
when ![]()
![]()

![]()
![]() ††††††††††††††††††††††††††††††††††† (111)
††††††††††††††††††††††††††††††††††† (111)
![]() †
†
![]()
Numerical illustration of Exact solution for Example 1
Applying exact solution technique to show the solution of the problem in example 1
![]() ††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (112)
††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (112)
![]() ††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (113)
††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (113)
when ![]() ,
, ![]()
when ![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (114)
†††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (114)
when ![]()
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (115)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (115)
![]() ††††
††††
Consider the differential equation:
![]() †††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (116)
†††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (116)
Solution
![]() †††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (117
†††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (117
![]() †††† ††††††††††† ††††††††††† (118)
†††† ††††††††††† ††††††††††† (118)
when ![]()
![]() †
†
 ††† (119)
††† (119)
![]() †† †(120)
†† †(120)
when ![]()
![]() ††††††††††††††††††††††††††††† ††††††††††† (121)
††††††††††††††††††††††††††††† ††††††††††† (121)
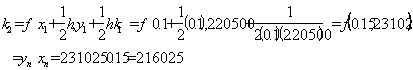 †††† ††††††††††† (122)
†††† ††††††††††† (122)
![]() †††††††††††††††††††††††† ††††††††††† (123)
†††††††††††††††††††††††† ††††††††††† (123)
when ![]()
![]() ††††††††††††††††††††††††† ††††††††††† (124)
††††††††††††††††††††††††† ††††††††††† (124)
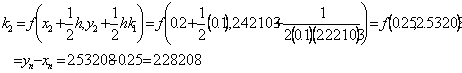 †††† (125)
†††† (125)
![]() †††††††††††††††††††††††††††††††††† ††††††††††† (126)
†††††††††††††††††††††††††††††††††† ††††††††††† (126)
![]()
Numerical illustration of exact solution for Example 2
Using exact solution approach to show the solution of the problem in example 2.
![]() ††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (127)
††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††† (127)
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (128)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† (128)
when ![]()
![]() †††††††††††† ††††††††††††††††††††††† ††††††††††† (129)
†††††††††††† ††††††††††††††††††††††† ††††††††††† (129)
when ![]()
![]() †††††††††††††† ††††††††††† (130)
†††††††††††††† ††††††††††† (130)
when ![]()
![]() †††††††††††† ††††††††††† (131)
†††††††††††† ††††††††††† (131)
![]()
Runge-Kutta method
From equation (49), Heunís method formula is thus given as:
![]() ††††† ††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (132)
††††† ††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† ††††††††††† (132)
where:
![]() †††††††††††††††††††††††††††††††† ††††††††††† (133)
†††††††††††††††††††††††††††††††† ††††††††††† (133)
Consider the differential equation of the initial value problem.
![]() †††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (134)
†††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (134)
Exact solution
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (135)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (135)
Solution
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (136)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† (136)
when ![]()
![]() ††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (137)†††
††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (137)†††
![]() ††††††††††††††††††††††† ††††††††††††††††††††††† (138)
††††††††††††††††††††††† ††††††††††††††††††††††† (138)
![]() ††††††††††††††††††††††††††††††††† ††††††††††† (139)
††††††††††††††††††††††††††††††††† ††††††††††† (139)
![]() ††† ††††††††††† ††††††††††††††††††††††† (140)
††† ††††††††††† ††††††††††††††††††††††† (140)
when ![]()
![]() ††††††††††††††††††††††††††††††††††† (141)
††††††††††††††††††††††††††††††††††† (141)
![]() †††††††††††††††† (142)
†††††††††††††††† (142)
![]() ††††††††††† ††††††††††† (143)
††††††††††† ††††††††††† (143)
†![]() † ††††††††††††††††††††††† (144)
† ††††††††††††††††††††††† (144)
![]() ††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (145)
††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (145)
When ![]() ††††††††††††††† †††††††††††
††††††††††††††† †††††††††††
![]() †††††††††† ††††††††††††††††††††††† (146)
†††††††††† ††††††††††††††††††††††† (146)
![]() ††††††††††††† (147)
††††††††††††† (147)
![]() ††††††††††††††††††††††† (148)
††††††††††††††††††††††† (148)
![]() † ††††††††††††††††††††††† (149)
† ††††††††††††††††††††††† (149)
![]() ††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††† (150)
††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††† (150)
![]()
Numerical illustration of exact solution for Example 1
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (151)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (151)
![]() ††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (152)
††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (152)
when ![]() †††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††
![]() ††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††† (153)
††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††† (153)
when ![]()
![]() †††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (154)
†††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (154)
when ![]()
![]() †††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (155)
†††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (155)
![]()
††††††††††† Consider the differential equation of the initial value problem:
![]() †††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (156)
†††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (156)
††††††††††† Exact solution
![]() ††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††† (158)
††††††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††††††††††††††† (158)
Solution:
![]() †††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (159)
†††††††††††††††††††††††††††††††††††††††††††††††††††††††† ††††††††††††††††††††††† (159)
![]() †††††††††††† ††††††††††† (160)
†††††††††††† ††††††††††† (160)
when ![]() †††††††††††††††††††††††††††††
†††††††††††††††††††††††††††††
![]() †† ††††††††††††††††††††††††††††††††††††††††††††††† †
††††††††† (161)
†† ††††††††††††††††††††††††††††††††††††††††††††††† †
††††††††† (161)
![]() †††††††††††† ††††††††††††††††††††††† (162)
†††††††††††† ††††††††††††††††††††††† (162)
![]() (163)
(163)![]() ††††††††††††††† (164)
††††††††††††††† (164)
when ![]()
![]() ††††††††††††††††††††††††††† ††††††††††† (165)
††††††††††††††††††††††††††† ††††††††††† (165)
![]() †††† ††††††††††† (166)
†††† ††††††††††† (166)
![]() † ††††††††††† (167)
† ††††††††††† (167)
![]() †††††††††††††††† (168)
†††††††††††††††† (168)
when ![]()
![]() ††††††††††††† ††††††††††††††††††††††† (169)
††††††††††††† ††††††††††††††††††††††† (169)
![]() †††††††††††††† (170)
†††††††††††††† (170)
![]() ††††††††††† (171)
††††††††††† (171)
![]() ††††††††††††††† (172)
††††††††††††††† (172)
![]()
Numerical illustration of exact solution for Example 2
![]() †††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (173)
†††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††† ††††††††††††††††††††††††††††††††††† (173)
![]() ††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††††††††††††††† (174)
††††††††††††††††††††††††††††††††††††††††††††† ††††††††††† ††††††††††††††††††††††††††††††††††† (174)
when ![]()
![]() ††††††††††† ††††††††††††††††††††††† ††††††††††† ††††††††††† (175)
††††††††††† ††††††††††††††††††††††† ††††††††††† ††††††††††† (175)
when ![]()
![]() †††††††††††††††††††††††††† (176)
†††††††††††††††††††††††††† (176)
when ![]() †
†
![]() †††††††††††† ††††††††††† (177)
†††††††††††† ††††††††††† (177)
![]() † (178)
† (178)
![]() †††††††††††††††††††††††††††††††††††††††††††††††† (179)
†††††††††††††††††††††††††††††††††††††††††††††††† (179)
Analysis of Euler and Runge-Kutta methods
The Euler and Runge-Kutta methods were compared by a rigorous analysis in order to demonstrate the efficiency of the methods to other techniques. The effect of the steps on the accuracy of the techniques was also examined.
The results obtained by solving some differential equations as considered in this paper were analyzed based on the theory of comparison. This help towards bringing out the result clearly for easy analysis and understanding of the established concept.
Results and Discussion
Standard Euler method
Table 1 showed that the results improved greatly when the standard Eulerís method was used. The tables below show the summary of all the results for the methods in consideration.
In comparing the two methods, we can see clearly that the Euler method is more preferable than the Runge-Kutta, especially when many values of xn are required. If only a few values of xn are needed, then the Runge-Kutta techniques is preferred to Euler method because it gives slightly better results
Table 1. Solution
for ![]()
|
N |
H |
f(xn, yn) |
yn+1 |
Exact solution |
Error |
|
0 |
0.1 |
0 |
1.00000 |
1 |
0 |
|
1 |
0.1 |
0.03 |
1.00300 |
1.00100 |
0.002 |
|
2 |
0.1 |
0.12036 |
1.01504 |
1.00803 |
0.00701 |
|
3 |
0.1 |
0.27406 |
1.04245 |
1.02730 |
0.01515 |
|
4 |
0.1 |
0.50038 |
1.09245 |
1.06609 |
0.02636 |
|
5 |
0.1 |
0.81938 |
1.17443 |
1.13315 |
0.04128 |
|
6 |
0.1 |
1.26838 |
1.30127 |
1.24110 |
0.06017 |
|
7 |
0.1 |
1.91287 |
1.49256 |
1.40917 |
0.08339 |
|
8 |
0.1 |
2.86572 |
1.77913 |
1.66863 |
0.1105 |
|
9 |
0.1 |
3.62692 |
2.14182 |
2.07301 |
0.06881 |
|
10 |
0.1 |
6.42546 |
2.78437 |
2.71828 |
0.06609 |
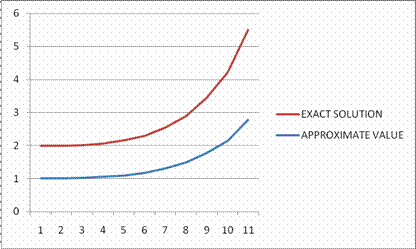
Figure 1. Graph of Approximate solution of standard Euler compare to exact solution
Table 2. Solution
for ![]()
|
N |
H |
f(xn, yn) |
yn+1 |
Exact number |
Error |
|
0 |
0.1 |
2.00000 |
2.20000 |
2.0000 |
0.2 |
|
1 |
0.1 |
2.10000 |
2.41000 |
2.20517 |
0.20483 |
|
2 |
0.1 |
2.21000 |
2.61000 |
2.42140 |
0.1886 |
|
3 |
0.1 |
2.33100 |
2.86410 |
2.64986 |
0.21424 |
|
4 |
0.1 |
2.46410 |
3.11051 |
2.89182 |
0.21869 |
|
5 |
0.1 |
2.61051 |
3.37156 |
3.14872 |
0.22284 |
|
6 |
0.1 |
2.77156 |
3.64872 |
3.42212 |
0.2266 |
|
7 |
0.1 |
2.94872 |
3.94360 |
3.71375 |
0.22985 |
|
8 |
0.1 |
3.14360 |
4.25796 |
4.02554 |
0.23242 |
|
9 |
0.1 |
3.35796 |
4.59376 |
4.35960 |
0.23416 |
|
10 |
0.1 |
3.56376 |
4.95314 |
4.71828 |
0.23486 |
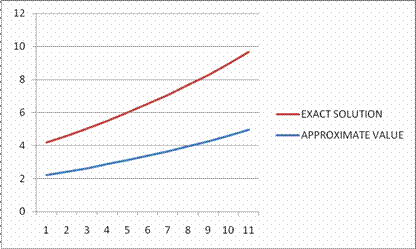
Figure 2. Graph of Approximate solution of standard Euler compared to exact solution
Modified Euler Method
The performance of the modified Euler method is presented in Table 3 and 4 and graphically depicted in Figure 3 and 4.
Table 3. Solution
for ![]()
|
N |
H |
f(xn, yn) |
yn+1 |
Exact number |
Error |
|
0 |
0.1 |
0.00000 |
1.00075 |
2.0000 |
0.99925 |
|
1 |
0.1 |
0.03002 |
1.00750 |
2.20517 |
1.19767 |
|
2 |
0.1 |
0.12090 |
1.08352 |
2.42140 |
1.33788 |
|
3 |
0.1 |
0.29255 |
1.12076 |
2.64986 |
1.5291 |
|
4 |
0.1 |
0.53769 |
1.19050 |
2.89182 |
1.70132 |
|
5 |
0.1 |
0.89288 |
1.30259 |
3.14872 |
1.84613 |
|
6 |
0.1 |
1.40680 |
1.47661 |
3.42212 |
1.94551 |
|
7 |
0.1 |
2.17062 |
1.74410 |
3.71375 |
1.96965 |
|
8 |
0.1 |
3.34867 |
2.15842 |
4.02554 |
1.86712 |
|
9 |
0.1 |
5.24496 |
2.81384 |
4.35960 |
1.54576 |
|
10 |
0.1 |
8.44151 |
3.88412 |
4.71828 |
0.83416 |
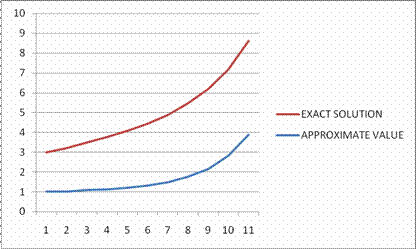
Figure 3. Graph of Approximate solution of Modified Euler compared to exact
Table 4. Solution
for†![]()
|
N |
H |
f(xn, yn) |
yn+1 |
Exact number |
Error |
|
0 |
0.1 |
2 |
2.20500 |
1 |
1.205 |
|
1 |
0.1 |
2.10500 |
2.42103 |
1.00100 |
1.42003 |
|
2 |
0.1 |
2.22103 |
2.62821 |
1.00803 |
1.62018 |
|
3 |
0.1 |
2.34924 |
2.89091 |
1.02730 |
1.86361 |
|
4 |
0.1 |
2.49091 |
3.15991 |
1.06609 |
2.09382 |
|
5 |
0.1 |
2.65991 |
3.43420 |
1.13315 |
2.30105 |
|
6 |
0.1 |
2.83420 |
3.72671 |
1.24110 |
2.48561 |
|
7 |
0.1 |
3.02679 |
4.03960 |
1.40917 |
2.63043 |
|
8 |
0.1 |
3.23960 |
4.37476 |
1.66863 |
2.70613 |
|
9 |
0.1 |
3.47476 |
4.73461 |
2.07301 |
2.6616 |
|
10 |
0.1 |
3.73461 |
5.12147 |
2.71828 |
2.40319 |
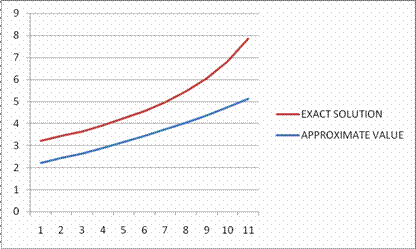
Figure 4. Graph of Approximate solution of Modified Euler compared to exact solution
Runge-Kutta method
The performances of the Runge-Kutta method are presented in Table 5 and 6 and graphically depicted in Figure 5 and 6.
Table 5. Solution
for![]()
|
N |
H |
f(xn, yn) |
yn+1 |
Exact number |
Error |
|
0 |
0.1 |
0 |
1.00100 |
1 |
0.001 |
|
1 |
0.1 |
0.3003 |
1.00802 |
1.00100 |
0.00702 |
|
2 |
0.1 |
0.12096 |
1.02730 |
1.00803 |
0.01927 |
|
3 |
0.1 |
0.27737 |
1.06587 |
1.02730 |
0.03857 |
|
4 |
0.1 |
0.55162 |
1.09345 |
1.06609 |
0.02736 |
|
5 |
0.1 |
0.82009 |
1.19691 |
1.13315 |
0.06376 |
|
6 |
0.1 |
1.29266 |
1.35754 |
1.24110 |
0.11644 |
|
7 |
0.1 |
1.99558 |
1.60456 |
1.40917 |
0.19539 |
|
8 |
0.1 |
3.08076 |
1.98746 |
1.66863 |
0.31883 |
|
9 |
0.1 |
4.82953 |
2.59376 |
2.07301 |
0.52075 |
|
10 |
0.1 |
7.78129 |
3.58510 |
2.71828 |
0.86682 |
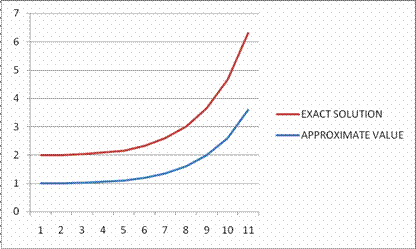
Figure 5. Graph of Approximate solution of Runge-kutta compared to exact solution
Table 6. Solution
for![]()
|
N |
H |
f(xn, yn) |
yn+1 |
Exact number |
Error |
|
0 |
0.1 |
1 |
1.7700 |
2.0000 |
0.23 |
|
1 |
0.1 |
1.67000 |
1.94035 |
2.20517 |
0.26482 |
|
2 |
0.1 |
1.74035 |
2.11809 |
2.42140 |
0.30331 |
|
3 |
0.1 |
1.81809 |
2.80399 |
2.64986 |
0.15413 |
|
4 |
0.1 |
1.90399 |
2.49891 |
2.89182 |
0.39291 |
|
5 |
0.1 |
1.99891 |
2.70380 |
3.14872 |
0.44492 |
|
6 |
0.1 |
2.10380 |
2.91970 |
3.42212 |
0.50242 |
|
7 |
0.1 |
2.21970 |
3.14777 |
3.71375 |
0.56598 |
|
8 |
0.1 |
2.34777 |
3.38929 |
4.02554 |
0.63625 |
|
9 |
0.1 |
2.48929 |
3.645667 |
4.35960 |
0.71393 |
|
10 |
0.1 |
2.64567 |
3.92094 |
4.71828 |
0.79734 |
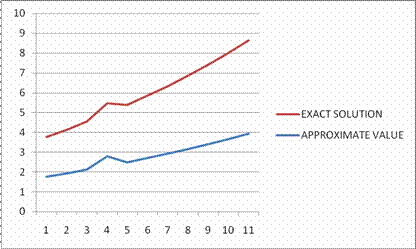
Figure 6. Graph of approximate solution of Runge-kutta compared to exact solution
Methods comparison
The performances of the methods for specific scenario are presented in Table 7 to 10 and graphically represented in Figure 7 to 10.
Table 7. Solution
for![]()
|
Runge-Kutta |
Standard Euler |
Modified Euler |
Exact Solution |
|
1.001 |
1 |
1.00075 |
1 |
|
1.00802 |
1.003 |
1.0075 |
1.001 |
|
1.0273 |
1.01504 |
1.08352 |
1.00803 |
|
1.06587 |
1.04245 |
1.12076 |
1.0273 |
|
1.09345 |
1.09245 |
1.1905 |
1.06609 |
|
1.19691 |
1.17443 |
1.30259 |
1.13315 |
|
1.35754 |
1.30127 |
1.47661 |
1.2411 |
|
1.60456 |
1.49256 |
1.7441 |
1.40917 |
|
1.98746 |
1.77913 |
2.15842 |
1.66863 |
|
2.59376 |
2.14182 |
2.81384 |
2.07301 |
|
3.5851 |
2.78437 |
3.88412 |
2.71828 |
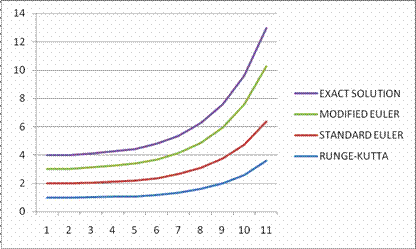
Figure 7. Comparison of Exact Solution, Standard Euler, Modified Euler and Runge-Kutta methods
Table 6. Solution
for![]()
|
Runge-Kutta |
Standard Euler |
Modified Euler |
Exact Solution |
|
1.77 |
2.2 |
2.205 |
1 |
|
1.94035 |
2.41 |
2.42103 |
1.001 |
|
2.11809 |
2.61 |
2.62821 |
1.00803 |
|
2.80399 |
2.8641 |
2.89091 |
1.0273 |
|
2.49891 |
3.11051 |
3.15991 |
1.06609 |
|
2.7038 |
3.37156 |
3.4342 |
1.13315 |
|
2.9197 |
3.64872 |
3.72671 |
1.2411 |
|
3.14777 |
3.9436 |
4.0396 |
1.40917 |
|
3.38929 |
4.25796 |
4.37476 |
1.66863 |
|
3.645667 |
4.59376 |
4.73461 |
2.07301 |
|
3.92094 |
4.95314 |
5.12147 |
2.71828 |
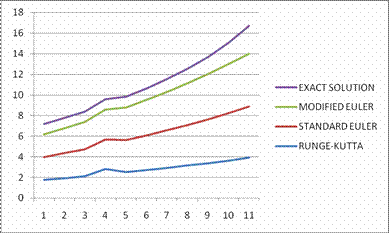
Figure 8. Comparison of Exact Solution, Standard Euler, Modified Euler and Runge-Kutta methods
Table 9. Absolute
Errors for![]()
|
Runge-Kutta |
Standard Euler |
Modified Euler |
|
0.001 |
0 |
0.99925 |
|
0.00702 |
0.002 |
1.19767 |
|
0.01927 |
0.00701 |
1.33788 |
|
0.03857 |
0.01515 |
1.5291 |
|
0.02736 |
0.02636 |
1.70132 |
|
0.06376 |
0.04128 |
1.84613 |
|
0.11644 |
0.06017 |
1.94551 |
|
0.19539 |
0.08339 |
1.96965 |
|
0.31883 |
0.1105 |
1.86712 |
|
0.52075 |
0.06881 |
1.54576 |
|
0.86682 |
0.06609 |
0.83416 |
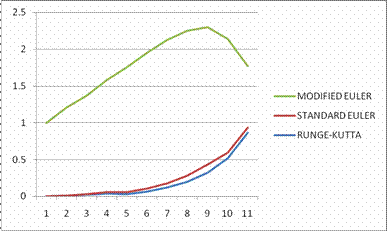
Figure 9.
Graph of Absolute Errors for Standard Euler, Modified Euler and Runge-Kutta methods
for ![]()
Table 10. Absolute
error for![]()
|
Runge-Kutta |
Standard Euler |
Modified Euler |
|
0.23 |
0.2 |
1.205 |
|
0.26482 |
0.20483 |
1.42003 |
|
0.30331 |
0.1886 |
1.62018 |
|
0.15413 |
0.21424 |
1.86361 |
|
0.39291 |
0.21869 |
2.09382 |
|
0.44492 |
0.22284 |
2.30105 |
|
0.50242 |
0.2266 |
2.48561 |
|
0.56598 |
0.22985 |
2.63043 |
|
0.63625 |
0.23242 |
2.70613 |
|
0.71393 |
0.23416 |
2.6616 |
|
0.79734 |
0.23486 |
2.40319 |
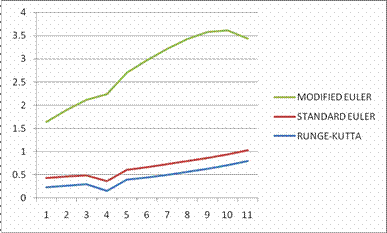
Figure 10.
Graph of absolute errors for Standard Euler, Modified Euler and Runge-Kutta methods
for ![]()
This research work has been carried out in order to compute direct solution of numerical method for order four of ordinary differential equations without reducing it to the system of first order differential equation through the application of both Euler and Runge-Kutta methods. These methods sufficiently reduce computational efforts as well as provide the accuracy needed in each result. It was analyzed from figures (1-10) and the percentage errors as (0.991% and 4.902% from Tables 1 and 2 for standard Euler method), (33.360% and 46.477% from Tables 3 and 4 for Modified Euler method) and (4.322% and 9.948% from Tables 5 and 6 for Runge-kutta method) which became necessary for a reasonable conclusion to be made.
Generally, the aim of a good numerical differentiation is that such methods should give better approximations to the true differentials. By the examples above, it shows that the two methods produced better degrees of accuracy for ordinary differential equations of all orders. But comparing the percentage errors, we discovered that Standard Euler method is more accurate than Modified Euler [3, 10, 11] and Runge-Kutta methods for the examples illustrated.
The exact solutions for both Euler and Runge-Kutta methods, whose values have the same order of accuracy with the derived solutions, were not only formulated, also tested for simplicity, efficiency and accuracy. We can conclude from the derivations above that the Standard Eulerís method has a higher degree of accuracy than the Modified Eulerís method, conclusion also supported by other studies [3, 10-15]. It is remarkable therefore to note that all the examples illustrated are differential equations of order four and orders which are less than four. This, to a large extent, reduces the effect that global error could have on the accuracy of the methods as obtained in tables (9 and 10) as well as the corresponding graphs in figures (9 and 10) respectively.
The methods were also examined to solve both linear and non-linear problems of the fourth order differential equations. Hence by percentage error, standard Euler method is ranked more accurate than Runge-kutta method with (0.991% and 4.902%), (4.322% and 9.948%) for the results in tables (1 and 2), (5 and 6) respectively.
References
1. Endre SMayer D. F., An introduction to Numerical Analysis, Cambridge University Press, 2003.
2. Hussain K., Ismail F., Senua N., Solving Direct Special First-Ordinary Differential Equations using Runge-Kutta, Journal of Computational and Applied Mathematics, 2016, p. 179-199.
3. Lanlege D. I., Garba U. M., Aluebho A., Using Modified Euler Method (MEM) for The solution of some First Order Differential Equations with Initial Value Problems (IVPs), Pacific Journal of Science and Technology, 2015, p. 63-81.
4. Leonarhd Euler., Standard Euler method: Available at: http://www.mathe.tufreiberg.de/~ernst/Lehre/Numerik_II/Folien/nadeChapter2.pdf (accessed 16/05/2017)
5. Bakhalou N. S., Numerical Methods, Mr. Publishing Company Inc., 1977.
6. Dormand J. R., Prince P. J., A reconsideration of some embedded Runge-Kutta Formulae, Journal of Computational and Applied Mathematics, 1986, 15, p. 203-211.
7. Hamming R. W., Numerical Methods for Scientists and Engineers, 2nd Edition, McGraw Hills Book, 1973.
8. Nystrom E. J., An Introduction to Numerical Methods, Oxford press Nigeria Plc, 1989.
9. Tracogna S., Jackiewicz, A General Class of Two Step Runge-Kutta Method for ODEs, Springer Series in Computational Mathematics, Verlang 2010, 10(4), p. 407-427.
10. Gerald C. E., Applied Engineering Mathematics, Addison Wesley Publishing Company Inc., 1970.
11. Lanlege D. I., Garba U. M., Gana U. M., Adetutu M. O., Application of Modified Euler Method (MEM) for solution of First Order Differential Equations with Initial Value Problems. Journal of Nigerian Association of Mathematical Physics, 2015, p 441-450.
12. Rivertz J., Ordinary Differential Equations Solved Exactly by Modified Euler Method, Archivum Mathematicum (BRNO), 2013, 49, p.29-34.
13. Taiwo O. A., Jimoh A. K., Bello A. K., Comparison of some Numerical Methods for the Solution of First and Second Orders Linear Integro Differential Equations, American Journal Of Engineering Research (AJER), 2014, 3(1), p. 245-250.
14. Zhang Y. A., Xiong Y., New Runge-Kutta Methods with Improved Internal Order, 2011, 820102. doi: 10.1117/12.904722.
15. Ababneh O. Y., Mossa A. M., Picard Approximation Method for Solving Nonlinear Quadratic Volterra Integral Equations, Journal of Mathematics Research, 2016, 8(1), p. 79-82.