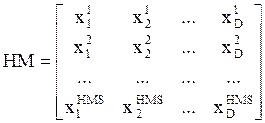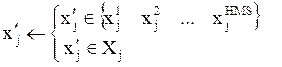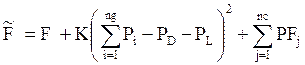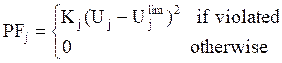Economic dispatch solution using efficient heuristic search approach
Samir SAYAH
QUERE Laboratory, Faculty of Technology, Electrical Engineering Department, Ferhat Abbas University, Setif 1, Algeria
E-mail: samir_sayah@yahoo.fr
Corresponding author, phone: +213561295179
Abstract
A new efficient hybrid differential evolution algorithm with harmony search (DE-HS) is proposed in this paper to solve the economic load dispatch (ELD) problem. The fresh individual generation mechanism of harmony search (HS) is utilized to enhance the local search capability of the original differential evolution (DE) method. The proposed hybrid algorithm is validated using the IEEE 30 bus test system and the practical Algerian 59 bus system. The results confirm the suitability of the proposed strategy to find accurate and feasible optimal solutions for ELD problems.
Keywords
Economic power dispatch (EPD); Differential Evolution (DE); Harmony Search (HS)
Introduction
Economic load dispatch is a fundamental function in modern power system operation and control. The conventional economic load dispatch (ELD) problem of power generation involves allocation of power output to different thermal units to minimize the operating cost subject to diverse equality and inequality constraints of the power system. This makes the ELD problem a large-scale highly nonlinear constrained optimization problem.
It is therefore of great importance to solve this problem as quickly and accurately as possible. Unfortunately, the input-output characteristics of modern units are inherently non-linear and non-convex because of valve-point loadings, prohibited operating zones and multiple fuels, and furthermore they may generate multiple local minimum points in the cost function. Conventional techniques offer good results, but when the search space is nonlinear and has discontinuities, these techniques become difficult to solve with a slow convergence ratio and not always seeking to the global optimal solution. New numerical methods are then needed to cope with these difficulties, specially, those with high speed search to the optimal and not being trapped in local minima.
The ELD problem has been solved via several traditional optimization methods including gradient-based techniques, newton methods, linear programming, and quadratic programming [1]. Most of these techniques are not capable to solve efficiently the optimization problems with a non-convex, non-continuous, and highly non-linear solution space.
Several heuristic global search tools have evolved in the last decades that have facilitated solving the ELD problems with non-smooth cost functions. Among these methods could be named the genetic algorithms [1, 2], evolutionary programming [3], neural networks [4], differential evolution [5], simulated annealing [6], tabu search [7], particle swarm optimization [8], and ant colony optimization [9]. Also the hybridization and combination of these methods have been used to solve more effectively ELD problems [10-12].
Differential evolution and harmony search algorithms are two of these global optimization techniques. Differential evolution (DE) algorithm which is inspired by biological and sociological motivations has been developed and introduced by Storn and Price [13] in 1995. DE algorithm improves a population of candidate solutions over several generations using the mutation, crossover and selection operators in order to reach an optimal solution [14]. In DE, the fitness of an offspring is one-to-one competed with that of the corresponding parent. This one-to-one competition makes convergence speed of DE faster than other evolutionary algorithms. Nevertheless, this faster convergence property yields in a higher probability of searching toward a local optimum or getting premature convergence [15-16].
Proposed by Geem et al. [17] in 2001, the harmony search (HS) method is inspired by the underlying principles of the musicians’ improvisation of the harmony. In the HS algorithm, musician improvises the pitches of his/her instrument to obtain a better state of harmony. The pitch of each musical instrument determines the aesthetic quality, just as the objective function value is determined by the set of values assigned to each decision variable [18]. On the other hand, HS is good at identifying the high performance regions of the solution space at a reasonable time. However, several studies [19-21] have shown that the original HS method has a limitation in dealing with the multimodal and constrained optimization problems.
To overcome the drawbacks of DE and HS, an efficient combination strategy of DE and HS (termed DE-HS) is introduced in this study. The proposed DE-HS consists essentially in a strong co-operation of DE and HS, since the DE-based update policy of existing individuals and HS-based generation strategy of new individuals are merged together [22].
In this study, a new efficient combined differential evolution and harmony search (DE-HS) algorithm is proposed for solving practical ELD problems. The performance of the proposed method is tested on two case studies using the IEEE 30 bus test system and the practical Algerian 59 bus system. Numerical results obtained by the proposed approach were compared with other optimization results reported in the literature recently.
Economic load dispatch problem formulation
The main objective of ELD is to minimize the total generation cost of the power system within a defined interval (typically 1h).
Objective function
The objective function for the ELD reflects the cost associated with generating power in the system. The objective function F for the entire power system can then be written as the sum of the fuel cost model for each generator:
|
F = |
(1) |
where Fi is the fuel cost function of the ith generator in ($/h) and ng is the number of online generating units to be dispatched.
Traditionally, the fuel cost curve is approximated using a simple smooth quadratic function [5] given by:
|
|
(2) |
where ![]() is the power of generator i.
is the power of generator i. ![]() ,
, ![]() and
and ![]() are the cost coefficients of generator i.
are the cost coefficients of generator i.
Power balance constraint
This constraint is based on the principle of equilibrium
between total system generation and total system loads ![]() and
transmission losses
and
transmission losses ![]() [5]. That is
[5]. That is
|
|
(3) |
where ![]() can
be obtained using the B matrix loss formula [5], given by:
can
be obtained using the B matrix loss formula [5], given by:
|
|
(4) |
where ![]() ,
, ![]() and
and
![]() are the loss coefficients.
are the loss coefficients.
Generator capacity constraints
For stable operation, the real power generation of each generator should be restricted between its lower and upper limits of generation. The generator capacity constraints are expressed as a pair of inequality constraints, as follows:
|
|
(5) |
Overview of differential evolution algorithm
The differential evolution algorithm (DE) is a population based algorithm like genetic algorithm using the similar operators; crossover, mutation and selection. In DE, each decision variable is represented in the chromosome by a real number. As in any other evolutionary algorithm, the initial population of DE is randomly generated, and then evaluated. After that, the selection process takes place. During the selection stage, three parents are chosen and they generate a single offspring which competes with a parent to determine which one passes to the following generation. DE generates a single offspring (instead of two like in the genetic algorithm) by adding the weighted difference vector between two parents to a third parent. If the resulting vector yields a lower objective function value than a predetermined population member, the newly generated vector replaces the vector to which it was compared.
An optimization task consisting of D parameters can be presented by a D-dimensional vector. In DE, a population of NP solution vectors is randomly created at the start. This population is successfully improved over G generations by applying mutation, crossover and selection operators, to reach an optimal solution [14, 15]. The main steps of the DE algorithm are given bellow:
Initialization
Evaluation
Repeat
Mutation
Crossover
Evaluation
Selection
Until (Termination criteria are met)
Initialization
Typically, each decision parameter in every vector of the initial population is assigned a randomly chosen value from within its corresponding feasible bounds:
|
|
(6) |
where ![]() denotes a uniformly distributed random number within the range [0,
1], generated anew for each value of j.
denotes a uniformly distributed random number within the range [0,
1], generated anew for each value of j. ![]() and
and ![]() are the upper and lower bounds of the jth decision parameter,
respectively.
are the upper and lower bounds of the jth decision parameter,
respectively.
Mutation
The mutation operator creates mutant vectors ![]() by perturbing a randomly
selected vector
by perturbing a randomly
selected vector ![]() with
the difference of two other randomly vectors
with
the difference of two other randomly vectors ![]() and
and![]() , according to the following equation
[17]:
, according to the following equation
[17]:
|
|
(7) |
where ![]() ,
, ![]() and
and![]() are randomly chosen vectors
among the NP population, and a ≠ b ≠ c.
are randomly chosen vectors
among the NP population, and a ≠ b ≠ c. ![]() ,
, ![]() and
and![]() are selected anew for each
parent vector. The scaling constant
are selected anew for each
parent vector. The scaling constant![]() is an algorithm control parameter used
to adjust the perturbation size in the mutation operator and improve algorithm
convergence.
is an algorithm control parameter used
to adjust the perturbation size in the mutation operator and improve algorithm
convergence.
Crossover
The crossover operation generates trial vectors ![]() by mixing the parameters of
the mutant vectors
by mixing the parameters of
the mutant vectors ![]() with
its target or parent vectors
with
its target or parent vectors![]() according to a selected probability
distribution of the following form [17]:
according to a selected probability
distribution of the following form [17]:
|
|
(8) |
where![]() denotes a
uniformly distributed random number within [0, 1], generated anew for each
value of j. q is a randomly chosen index
denotes a
uniformly distributed random number within [0, 1], generated anew for each
value of j. q is a randomly chosen index ![]() that guarantees that the trial vector
gets at least one parameter from the mutant vector. The crossover constant CR
is an algorithm parameter that controls the diversity of the population and
aids the algorithm to escape from local minima.
that guarantees that the trial vector
gets at least one parameter from the mutant vector. The crossover constant CR
is an algorithm parameter that controls the diversity of the population and
aids the algorithm to escape from local minima.
Selection
The selection operator forms the population by choosing between the trial vectors and their predecessors (target vectors) those individuals that present a better fitness or are more optimal according to (9) [17].
|
|
(9) |
This optimization process is repeated for several generations, allowing individuals to improve their fitness as they explore the solution space in search of optimal values.
DE has three essential control parameters which are: the scaling factor![]() , the crossover
constant CR and the population size NP. The scaling
factor is a value in the range [0, 2] that controls the amount of perturbation
in the mutation process. The crossover constant is a value in the range [0, 1]
that controls the diversity of the population. The population size determines
the number of individuals in the population and provides the algorithm enough
diversity to search the solution space.
, the crossover
constant CR and the population size NP. The scaling
factor is a value in the range [0, 2] that controls the amount of perturbation
in the mutation process. The crossover constant is a value in the range [0, 1]
that controls the diversity of the population. The population size determines
the number of individuals in the population and provides the algorithm enough
diversity to search the solution space.
Overview of harmony search algorithm
The harmony search (HS) is a music-inspired evolutionary algorithm, mimicking the improvisation process of music players searching for a perfect state of harmony [17-18]. The harmony in music is analogous to the solution vector and the behavior of musician’s improvisation is analogous to local and global search schemes in optimization techniques.
In the HS algorithm, musical performances seek a perfect state of harmony determined by aesthetic estimation, as the optimization algorithms seek a best state (i.e. global optimum) determined by objective function value. The optimization procedure of the HS algorithm consists of the following steps:
- Initialize algorithm parameters and harmony memory (HM).
- Improvise a new harmony from HM.
- Update harmony memory.
- Repeat Steps 3 and 4 until the stopping criterion is met.
The detailed description of these steps is summarized in the following [18]:
· Step 1. Initialize the HS Memory (HM). The initial HM consists of a certain number of randomly generated solutions for the optimization problem under consideration. For a D-dimension problem, an HM with the size of HMS can be represented as follows:
|
|
(10) |
where ![]() ( i =
1, 2, …, HMS ) is a solution candidate.
( i =
1, 2, …, HMS ) is a solution candidate.
· Step
2. Improvise a new solution ![]() from the HM. Each component of this
solution,
from the HM. Each component of this
solution,![]() ,
is obtained based on the harmony memory considering rate (HMCR). The HMCR is
defined as the probability of selecting a component from the present HM
members, and 1–HMCR is, therefore, the probability of generating it randomly:
,
is obtained based on the harmony memory considering rate (HMCR). The HMCR is
defined as the probability of selecting a component from the present HM
members, and 1–HMCR is, therefore, the probability of generating it randomly:
|
j =1, 2, …, D |
(11) |
where ![]() is the set of the
possible range of values for the jth decision parameter.
is the set of the
possible range of values for the jth decision parameter.
After, every component ![]() obtained
from the HM is examined to determine whether it should be pitch-adjusted. This
operation uses the PAR parameter, which is the pitch adjustment rate as
follows:
obtained
from the HM is examined to determine whether it should be pitch-adjusted. This
operation uses the PAR parameter, which is the pitch adjustment rate as
follows:
|
|
(12) |
The PAR determines the probability of a candidate from
the HM to be mutated. The value of ![]() sets the rate of
doing nothing. If the pitch adjustment decision for
sets the rate of
doing nothing. If the pitch adjustment decision for ![]() is Yes, then
is Yes, then ![]() is replaced as
follows:
is replaced as
follows:
|
|
(13) |
where bw is an arbitrary distance bandwidth and ![]() is
a random number generated using uniform distribution between 0 and 1.
is
a random number generated using uniform distribution between 0 and 1.
· Step 3. Update the HM. First, the new solution from Step 2 is evaluated. If it yields a better fitness than that of the worst member in the HM, it will replace that one. Otherwise, it is eliminated.
· Step 4. Repeat Step 2 to Step 3 until a termination criterion (e.g., maximal number of iterations) is met.
HS method is a random search technique which it does not require any prior domain information, such as the gradient of the objective functions. However, different from those population-based evolutionary approaches, it only utilizes a single search memory to evolve. Therefore, the HS method has the interesting characteristics of algorithm simplicity.
Hybridization of differential evolution and harmony search
During the past decade, hybridization of evolutionary algorithms has gained growing popularity, which can overcome their individual drawbacks while benefit from each other’s strengths [15, 22]. In this context, Gao et al. [22] have proposed a new hybrid optimization technique, namely DE-HS, by embedding the HS into the DE method.
Both the DE and HS have their advantages and weakness. Especially, the DE updates the current individuals based on only the differences among certain randomly selected ones. Unfortunately, it does not have an explicit mechanism for generating new chromosomes. On the other hand, the HS method has the distinguishing feature of using the combination of all the existing ones to obtain fresh individuals. Therefore, a natural idea is to embed this individual generation approach into the original DE so that it can converge in a faster way [22].
The iteration procedure of the DE-HS can be explained as follows [22]. The chromosomes in the DE population are first updated according to the DE principle in (6), (7) and (8). Next, these chromosomes are considered as the harmony memory members of the HS method. Note that the size of the HM is the same as that of the DE population, i.e., HMS = NP. Thus, a new individual is produced either based on the HM members (DE population) or in a random manner as in Step 2 of HS algorithm. The key HS parameters, HMCR and PAR, are also used here. This fresh candidate is then compared with the worst DE individual for possible replacement as in Step 3 of the HS method. Finally, the whole population is updated, and the DE evolution continues to the next iteration. It can be seen from the above description that the DE and HS are complementary rather than competitive with each other. Incorporating the HS-based new individual generation strategy into the DE can indeed enhance its local exploration in the search space and result in a superior optimization performance.
The stopping criteria are the conditions under which the search process will stop. In this work, the search procedure will terminate whenever the predetermined maximum number of iterations Gmax is reached, or whenever the global best solution does not improve over a predetermined number of iterations.
Constraints handling
It is worth mentioning that the control variables are self-constrained. In order to keep the trial vectors within their bounds, the control parameter that exceeds a feasible bound is adjusted to the corresponding violated bound.
A penalty function approach is used to handle the power
balance constraint and inequality constraints. The
extended objective function ![]() (or fitness function)
is defined by:
(or fitness function)
is defined by:
|
|
(14) |
where K
denotes the penalty factor of the equality constraint; nc represents the
number of inequality constraints and ![]() is the penalty function for the jth
inequality constraint; given as:
is the penalty function for the jth
inequality constraint; given as:
|
|
(15) |
Kj is
the penalty factor for the jth inequality constraint; ![]() is the limit value of
the variable
is the limit value of
the variable![]() .
.
Results and Discussion
The proposed DE-HS approach was tested using the
IEEE 30 bus benchmark system [16] and the practical Algerian 59-bus system
[24]. In order to compare the results obtained from DE-HS, optimization
problems are also solved using the conventional DE and HS methods. For all
optimization methods (DE-HS, DE and HS), 50 independent runs were made in each
case study using the same control parameter settings, as follows: population size (or HM size) NP = HMS = 20,
mutation factor ![]() = 0.50, crossover constant CR
= 0.99, HM considering rate HMCR = 0.99, pitch adjustment rate
PAR = 0.10, distance bandwidth bw = 0.05 and maximum number of
iterations Gmax = 1000. All the programs were implemented under the
MATLAB computational environment, on an Intel Core 2 Duo 2.10
GHz Laptop computer with 3 GB RAM under Windows 7.
= 0.50, crossover constant CR
= 0.99, HM considering rate HMCR = 0.99, pitch adjustment rate
PAR = 0.10, distance bandwidth bw = 0.05 and maximum number of
iterations Gmax = 1000. All the programs were implemented under the
MATLAB computational environment, on an Intel Core 2 Duo 2.10
GHz Laptop computer with 3 GB RAM under Windows 7.
Case 1: Results for the IEEE 30 bus system
The IEEE 30 bus – 6 generators test system is described in [23], where the total load was set to 283.40 MW. Table 1 shows the data for the six generators. Over 50 repeated trials, the average solution cost achieved by DE-HS was 803.11 $/h with a minimum cost of 803.10 $/h, and a maximum cost of 803.18 $/h (0.0099% difference). The average execution time was 0.15 second. Table 2 gives the solution details for a minimum cost, which converged after 40 iterations and 0.14 second. It is important to point out that all variables were able to stay within their permissible limits sown in Table 1. The convergence of DE-HS for the trial run with the minimum fuel cost is shown in Fig. 1.
Table 1. Generators data of the IEEE 30 bus system
|
Parameter |
Gen. 1 |
Gen. 2 |
Gen. 3 |
Gen. 4 |
Gen. 5 |
Gen. 6 |
|
a ($/Mw2 h) |
0.00375 |
0.0175 |
0.0625 |
0.00834 |
0.025 |
0.025 |
|
b ($/MWh) |
2.00 |
1.75 |
1.00 |
3.25 |
3.00 |
3.00 |
|
c ($/h) |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
50 |
20 |
15 |
10 |
10 |
12 |
|
|
200 |
80 |
50 |
35 |
30 |
40 |
|
a, b and c = cost coefficients |
||||||
Table 2. The best economic dispatch solution found by DE-HS for case 1
|
Parameter |
Value |
|
P1 (MW) |
177.70 |
|
P2 (MW) |
48.43 |
|
P3 (MW) |
20.99 |
|
P4 (MW) |
21.46 |
|
P5 (MW) |
12.60 |
|
P6 (MW) |
12.00 |
|
Total power generation (MW) |
293.19 |
|
Total power demand (MW) |
283.40 |
|
Fuel cost ($/h) |
803.10 |
|
Loss (MW) |
9.79 |
|
Execution time (s) |
0.14 |
Table 3 presents the comparison of the minimum, maximum, mean cost, mean iteration and average computation time for the simulation over 50 trial runs obtained by the proposed hybrid DE-HS with the DE and HS algorithms. As seen from Table 3, the best, worst and average solutions obtained with the proposed DE-HS algorithm are better than the best, worst and average results of all other methods. It is observed that the best solution found by DE-HS is identical to that found by DE. Besides, the mean cost given by DE-HS is better compared to other methods. From Table 3, it is also clear that the suggested method converges in less iterations (43 iterations) compared to the conventional DE (63 iterations) and HS (578 iterations). The minimum cost and maximum cost are very close (0.0099% difference) indicating a good convergence characteristic and a great robustness of the proposed hybrid DE-HS.
Table 3. Comparison results of the three methods (DE-HS, DE and HS) for case 1
|
Method |
Minimum cost ($/h) |
Maximum cost ($/h) |
Mean cost ($/h) |
Mean iteration |
Average CPU Time (s) |
|
HS |
804.58 |
833.38 |
816.59 |
578 |
0.07 |
|
DE |
803.10 |
803.55 |
803.15 |
63 |
0.20 |
|
DE-HS |
803.10 |
803.18 |
803.11 |
43 |
0.15 |
|
HS = Harmony Search; DE = Differential Evolution |
|||||
Fig. 1 represents the convergence curves of the best solutions found by DE-HS, DE and HS. This figure shows that DE-HS converges well and has the better convergence behavior than the DE and HS. This faster convergence behavior of the proposed DE-HS is due to the incorporation of the HS individual generation strategy into the original DE which enhances the local search capability of the original DE method.
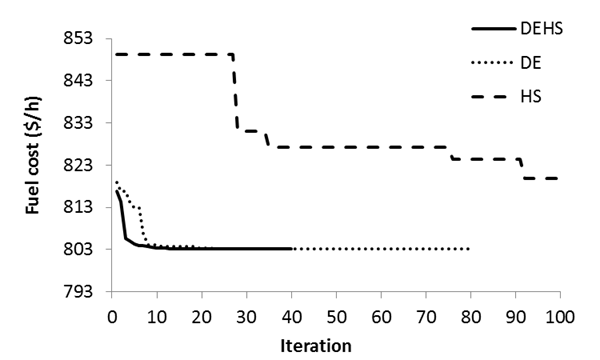
Figure 1. Comparison of the convergence curves of DE-HS, DE (Differential Evolution), and HS (Harmony Search) (case 1)
The results of the proposed approach were compared in Table 4 to those reported using Gradient Projection Method (GPM) [23], Nonlinear Programming (NLP) [25], Evolutionary Programming (EP) [26], Improved Particle Swarm optimization (IPSO) [27], and Improved Evolutionary Programming (IEP) [28]. It can be seen that the results given by DE-HS are close to those reported in the literature. As a conclusion, we can say that the suggested DE-HS has the ability to find acceptable solutions in a reasonable time compared to other approaches which allow to an online implementation.
Table 4. Comparison of simulation results for the IEEE 30 bus system
|
Parameters |
GPM [23] |
NLP [25] |
EP [26] |
IPSO [27] |
IEP [28] |
HS |
DE |
DE-HS |
|
187.22 |
176.26 |
173.85 |
179.37 |
176.24 |
168.46 |
177.51 |
177.70 |
|
|
P2 (MW) |
53.78 |
48.84 |
49.99 |
44.24 |
49.01 |
47.16 |
48.43 |
48.43 |
|
P3 (MW) |
16.95 |
21.51 |
21.39 |
24.61 |
21.50 |
19.91 |
20.86 |
20.99 |
|
P4 (MW) |
11.29 |
22.15 |
22.63 |
19.90 |
21.811 |
27.23 |
21.78 |
21.46 |
|
P5 (MW) |
11.29 |
12.14 |
12.93 |
10.71 |
12.34 |
13.68 |
12.59 |
12.60 |
|
P6 (MW) |
13.35 |
12.00 |
12.00 |
14.09 |
12.01 |
16.09 |
12.00 |
12.00 |
|
Total Gen. (MW) |
293.88 |
292.90 |
292.79 |
292.92 |
292.9105 |
292.53 |
293.17 |
293.19 |
|
Cost ($/h) |
804.85 |
802.40 |
802.62 |
803.69 |
802.465 |
804.58 |
803.10 |
803.10 |
|
Loss (MW) |
10.49 |
9.48 |
- |
9.52 |
- |
9.13 |
9.78 |
9.80 |
|
CPU time (s) |
4.32 |
- |
51.4 |
7.00 |
594.08 |
0.10 |
0.20 |
0.14 |
|
GPM = Gradient Projection Method; NLP = Nonlinear Programming; EP = Evolutionary Programming; IPSO = Improved Particle Swarm optimization; IEP = Improved Evolutionary Programming; HS = Harmony Search; DE = Differential Evolution |
||||||||
Case 2: Results for the practical Algerian 59 bus system
The Algerian network consists of 59 buses and 10 generators supplying a total load of 684.10 MW [24]. Table 5 provides the parameters associated with the generating units (it is noting that the generator no. 5 at bus no. 13 is not operational).
The results found by DE-HS were compared in Table 6 with the results of DE and HS methods. From the comparative results of Table 6, it is evident that the hybrid DE-HS outperforms all other methods in terms of achieving successfully the best mean cost of 1712.12 $/h with less iterations and less computation time than the original DE. It is also observed that the minimum and maximum costs achieved by DE-HS are very close, which gives a clear indication of stability of the results and robustness of the proposed strategy.
Table 5. Generator parameters of the Algerian network
|
Bus |
Gen. |
(MW) |
(MW) |
a ($/MW2h) |
b ($/MWh) |
c ($/h) |
|
1 |
1 |
8 |
72 |
0.0085 |
1.50 |
0 |
|
2 |
2 |
10 |
70 |
0.0170 |
2.50 |
0 |
|
3 |
3 |
30 |
510 |
0.0085 |
1.50 |
0 |
|
4 |
4 |
20 |
400 |
0.0085 |
1.50 |
0 |
|
13 |
5 |
15 |
150 |
0.0170 |
2.50 |
0 |
|
27 |
6 |
10 |
100 |
0.0170 |
2.50 |
0 |
|
37 |
7 |
10 |
100 |
0.0030 |
2.00 |
0 |
|
41 |
8 |
15 |
140 |
0.0030 |
2.00 |
0 |
|
42 |
9 |
18 |
175 |
0.0030 |
2.00 |
0 |
|
53 |
10 |
30 |
450 |
0.0085 |
1.50 |
0 |
|
|
||||||
Table 6. Comparison results of the three methods (DE-HS, DE and HS) for case 2
|
Method |
Minimum cost ($/h) |
Maximum cost ($/h) |
Mean cost ($/h) |
Mean iteration |
Average CPU Time (s) |
|
HS |
1712.17 |
1728.30 |
1713.94 |
986 |
0.09 |
|
DE |
1712.18 |
1724.51 |
1714.32 |
208 |
0.35 |
|
DE-HS |
1712.10 |
1712.20 |
1712.12 |
59 |
0.16 |
HS = Harmony Search; DE = Differential Evolution
The convergence characteristics of DE-HS, DE and HS are depicted in Fig. 2. It is quite clear that the proposed DE-HS approach has a faster convergence rate.
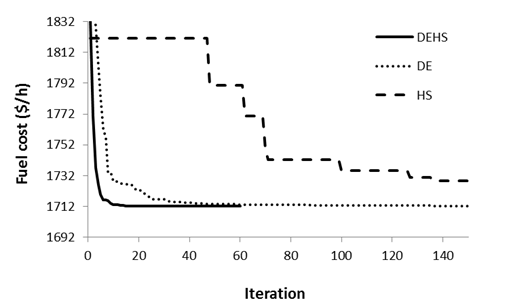
Figure 2. Convergence behaviour of DE-HS, DE (Differential Evolution) and HS (Harmony Search) algorithms (case 2)
The results of the proposed approach were compared to those reported using genetic algorithm (GA) [24] and ant colony optimization method (ACO) [29]. The comparison results are given in Table 7. From this table, it can be seen that the proposed approach gives better results with a very short computation time and the saving in fuel cost is significant. This demonstrates the potential and effectiveness of the proposed method to solve the nonlinear optimization problems.
Table 7. Comparison of simulation results for the Algerian network
|
Parameters |
GA [13] |
ACO [14] |
HS |
DE |
DE-HS |
|
P1 (MW) |
70.57 |
64.01 |
55.64 |
54.45 |
54.80 |
|
P2 (MW) |
56.57 |
22.75 |
24.13 |
24.18 |
25.01 |
|
P3 (MW) |
89.27 |
82.37 |
104.62 |
103.51 |
104.69 |
|
P4 (MW) |
78.22 |
46.21 |
112.32 |
114.77 |
112.72 |
|
P5 (MW) |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
|
P6 (MW) |
57.93 |
47.05 |
27.39 |
26.36 |
27.24 |
|
P7 (MW) |
39.55 |
65.56 |
57.47 |
57.42 |
57.11 |
|
P8 (MW) |
46.40 |
39.55 |
91.84 |
89.79 |
89.83 |
|
P9 (MW) |
63.58 |
154.23 |
139.57 |
140.36 |
140.01 |
|
P10 (MW) |
211.58 |
202.36 |
105.80 |
107.19 |
106.60 |
|
Total Generation (MW) |
713.67 |
724.09 |
718.78 |
718.02 |
718.02 |
|
Cost ($/h) |
1937.10 |
1815.70 |
1712.17 |
1712.18 |
1712.10 |
|
Loss (MW) |
29.58 |
39.98 |
34.69 |
33.93 |
33.93 |
|
CPU time (s) |
3.10 |
25.00 |
0.10 |
0.30 |
0.16 |
|
GA = Genetic Algorithm; ACO = Ant Colony Optimization; HS = Harmony Search; DE = Differential Evolution |
|||||
Conclusions
Incorporating the HS-based new individual generation strategy into the DE can indeed enhance its local exploration in the search space and result in a superior optimization performance.
Computational results show that the proposed hybrid approach has the ability to converge to high quality solutions with stable convergence characteristic and good computation efficiency.
Considering the cases and comparative study presented in this paper, DE-HS algorithm appears to be very efficient in particular for its fast convergence to the global optimum and its interesting financial profit. This method is highly appropriate for on-line applications in power systems.
References
1. Walters D. C., Sheble G. B., Genetic algorithm solution of economic dispatch with valve point loading, IEEE Trans. Power Systems, 1993, 8, p. 1325-1332.
2. Chiang C. L., Improved genetic algorithm for power economic dispatch of units with valve-point effects and multiple fuels, IEEE Trans. Power Systems, 2005, 20, p. 1690-1699.
3. Sinha N., Chakrabarti R., Chattopadhyay P. K., Evolutionary programming techniques for economic load dispatch, IEEE Trans. Evolutionary Computation, 2003, 7, p. 83-94.
4. Park J. H., Kim Y. S., Eom I. K., Lee K. Y, Economic load dispatch for piecewise quadratic cost function using hopfield neural network, IEEE Trans. Power Systems, 1993, 8, p. 1030-1038.
5. Noman N., Iba H., Differential evolution for economic load dispatch problems, Electric Power Systems Research, 2008, 78, p. 1322-1331.
6. Wong K. P., Fung C. C, Simulated annealing based economic dispatch algorithm, IEE Proc. Gener. Transm. Distrib., 1993, 140, p. 509-515.
7. Lin W. M., Cheng F. S., Tsay M.T., An improved tabu search for economic dispatch with multiple minima, IEEE Trans. Power Systems, 2002, 17, p. 108-112.
8. Park J. B., Lee K. S., Shin J. R., Lee K. Y., A particle swarm optimization for economic dispatch with non-smooth cost functions, IEEE Trans. Power Systems, 2005, 20, p. 34-42.
9. Pothiya S., Ngamroo I., Kongprawechnon W., Ant colony optimization for economic dispatch problem with non-smooth cost functions, Electrical Power and Energy Systems, 2010, 32, p. 478-487.
10. He D., Wang F., Mao Z., A hybrid genetic algorithm approach based on differential evolution for economic dispatch with valve-point effect, Electrical Power and Energy Systems, 2008, 30, p. 31-38.
11. Ongsakul W., Ruangpayoongsak N., Constrained dynamic economic dispatch by simulated annealing/genetic algorithms, IEEE Power Eng. Soc. Innovative Computing for Power-Electric Energy Meets the Market Conference, Sydney, NSW, 2001, p. 207-212.
12. Wang S. K., Liu C. W., Chiou J. P., Ant direction hybrid differential evolution for solving economic dispatch of power system, in Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, Taipei, Taiwan, 2006, p. 1154-1159.
13. Storn R., Price K., Differential evolution – a simple and efficient adaptive scheme for global optimization over continuous spaces, Journal of Global Optimization, 1997, 11, p. 341-359.
14. Storn R., On the usage of differential evolution for function optimization, in Proceedings of the Biennial Conference of the North American Fuzzy Information Processing Society NAFIPS, Berkley, 1996, p. 519-523.
15. He D., Wang F., Mao Z., A hybrid genetic algorithm approach based on differential evolution for economic dispatch with valve-point effect, Electrical Power and Energy Systems, 2008, 30, p. 31-38.
16. Sayah S., Zehar K., Modified differential evolution algorithm for optimal power flow with non-smooth cost functions, Energy Conversion and Management, 2008, 49, p. 3036-3042.
17. Geem Z. W., Kim J. H., Loganathan G. V., A new heuristic optimization algorithm: harmony search, Simulation, 2001, 76, p. 60-68.
18. Lee K. S., Geem Z. W., A new meta-heuristic algorithm for continuous engineering optimization: harmony search theory and practice, Computer Methods in Applied Mechanics and Engineering, 2005, 194, p. 3902-3933.
19. Omran M. G. H., Mahdavi M., Global-best harmony search, Applied Mathematics and Computation, 2008, 198, p. 643-656.
20. Mahdavi M., Fesanghary M., Damangir E., An improved harmony search algorithm for solving optimization problems, Applied Mathematics and Computation, 2007, 188, p. 1567-1579.
21. Coelho L. S., Mariani V. C., An improved harmony search algorithm for power economic load dispatch, Energy Conversion and Management, 2009, 50, p. 2522-2526.
22. Gao X. Z., Wang X., Ovaska S. J., A harmony search-based differential evolution method, in Proceedings of The 13th IEEE International Conference on Computational Science and Engineering, Hong Kong, China, 2010, p. 333-339.
23. Lee K., Park Y., Ortiz J., A United Approach to Optimal Real and Reactive Power Dispatch, IEEE Trans. on Power Apparatus and Systems, 1985, 104, p. 1147-1153.
24. Bouktir T., Slimani L., Optimal Power Flow of the Algerian Network Using Genetic Algorithms, WSEAS Trans. Circuit and Systems, 2004, 3, p. 1478-1482.
25. Alsac O., Stott B., Optimal Load Flow with Steady-State Security, IEEE Trans. on Power Apparatus and Systems, 1974, 93, p. 745-751.
26. Yuryevich J., Wong K. P., Evolutionary Programming Based Optimal Power Flow Algorithm, IEEE Trans. Power Systems, 1999, 14, p. 1245-1250.
27. Bouktir T., Slimani L., A Genetic Algorithm for Solving the Optimal Power Flow Problem, Leonardo Journal of Sciences, 2004, 4, p. 44-58.
28. Ongsakul W., Tantimaporn T., Optimal Power Flow by Improved Evolutionary Programming, Electric Power Components and Systems, 2006, 34, p. 79-95.
29. Bouktir T., Slimani L., Optimal Power Flow of the Algerian Electrical Network Using an Ant Colony Optimization Method, in Proceedings of the 9th IASTED International Conference on Artificial Intelligence and Soft Computing, Benidorm, Spain, 2005.
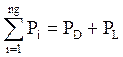
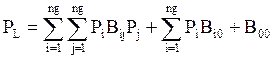
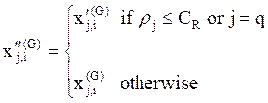 , i = 1, …,
NP, j = 1,…, D
, i = 1, …,
NP, j = 1,…, D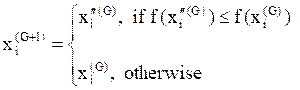 , i = 1, …, NP
, i = 1, …, NP