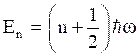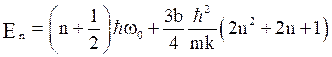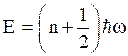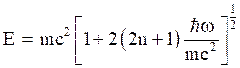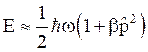One dimensional harmonic oscillators revisited
Nilesh P. BARDE1, Pranav P. BARDAPURKAR2*
1Department of Physics, Badrinarayan Barwale Mahavidyalaya, Jalna, Maharashtra, India,
2* Department of Physics, S. N. Arts, D.J. Malpani Commerce & B. N. Sarda Science College, Sangamner, Maharashtra, India
E-mail(s): nilesh_barde123@rediffmail.com; * ppbardapurkar@rediffmail.com
* Corresponding author: +919420808535
Abstract
The concept of harmonic oscillator particularly one dimensional (1-D) is mentioned in literature repeatedly and is explained in more complex manner by using various methods. This creates difficulties in understanding the description of the concept for new learners. The purpose of this article was to enlighten different methods to formulate harmonic oscillator in improving knowledge about detailed steps to derive eigen energy values in more comprehensible manner for the beginners. The energy values are derived by using classical method, quantum mechanically, Schrodinger time independent equation, perturbation technique, variation method, WKB approximation etc. A coherent way of derivation of eigen values using various approaches makes this article as unique.
Keywords
Harmonic oscillator; Wave function; Hamiltonian; Eigen value
Introduction
Most of the physical phenomena studied till the Einstein’s era was related to the macroscopic world. The laws of nature discovered were all from the Newtonian mechanics. The classical physics was concerned with those aspect of nature for which question of the ultimate constitution of matter was not of immediate concern. Classical theories are phenomenological theories which attempt to describe and summarize experimental facts in limited domain of physics. But, in the case of microscopic world, it has been proved that classical theories were not of universal validity [[1]-[3]]. These laws describe behavior of mechanism of rigid bodies with respect to some material constants such as density, elasticity etc. But they are unable to explain why density has that value at certain specific physical condition, why wire breaks after exceeding limits, etc. It also fails to explain why metallic rod turns white from red when temperature is increased. These problems bring revolution in physics through the discovery of quantum mechanics, which was a total surprise to the scientists. It describes the physical world in a way that was fundamentally new. In early stages, quantum theory seems to be a poor substitute for classical laws, but later from various experiments it was realized by the scientific community. In this paper special emphasis is given on the main building blocks of quantum mechanics which solve many problems, which in turn helps in developing various concepts in modern physics [[4]-[7]].
After the discovery of radiators of energy bundles for black body radiations by Max Planck in 1900, many quantum mechanical systems were evolved. The harmonic oscillator is one of the most important quantum systems which can be solved more accurately and hence is of great interest. Harmonic oscillator in one dimension (1-D) is an excellent tool to introduce methods of solving various second order Schrodinger’s differential equations occurring in different problems in quantum theory. This concept had been in use since classical era to study vibrations of atoms or molecules in various conditions in solids. After the development of quantum theory in last century, people are now aware about the building block rules [[8]-[11]]. But, the quantum behavior of free particles or particles constrained inside different potentials cannot be determined easily. Setting up such problem in terms of harmonic oscillator system helps to calculate required energy levels.
We are familiar that among all other branches in Physics, quantum mechanics is an essential branch which got enormous fame in first half of 20th century, before which people were in belief for laws of classical mechanics. When students entered in undergraduate level of their studies, they were having a high impact of Newtonian mechanical laws. At higher studies, when these students came across concepts from quantum mechanics, it seems to be contradictory to the conventional theories. Hence many times various concepts of quantum theories become difficult to deal with. There are hardly any efforts are taken to resolve issues while tackling large derivations particularly for a problem of harmonic oscillator [[12]-[17]].
Many researchers attempted to bridge the gap and tried to solve problems in easier way, but with individual techniques. This pitfall itself is a motivation for present work. Thrust of this paper is to explore the theory of harmonic oscillator at a glance, which common readers seek to comprehend the mysterious world of quantum physics. The main advantage of this article is that the derivations are discussed in the light of implications for novices who have a keen interest to know more about the field. It is the authors’ view to introduce various ways of deriving 1-D harmonic oscillator equations without any prerequisite knowledge of quantum mechanics. This paper summarizes derivations of 1-D harmonic oscillator with detailed description of equations used along with their significance and elaborating simple mathematical steps involved in deriving it. It is an attempt to highlight basic concepts in quantum mechanics initializing from an empirical relation such as kinetic energy, potential functions, Hamiltonian, wave functions etc of the system and their applications in evaluating eigen energy values. Though a reader may find it much detailed, it is essential to present all the derivational steps to cater the needs of a beginner.
Material and method
Harmonic oscillator performs undamped simple harmonic motion which is periodic with constant amplitude. The main features of harmonic oscillator; though they may be considered in various conditions, are its positive amplitude, periodicity, its phase determination and frequency, on the basis of which wave function can be assumed. Harmonic oscillator is always defined in terms of second order differential equation whose solution is to be assumed to evaluate the energy levels. Classically, initial energy of the oscillator is due to its restoring force, which brings oscillator to the equilibrium position when displaced. But, quantum mechanically; the initial energy is determined in terms of a Hamiltonian, which consists of kinetic and potential energies of the system [[18]-[21]].
The steps involved in determining energy eigen values for 1-D harmonic oscillators with different methods is highlighted in the flow chart shown in Fig. 1.
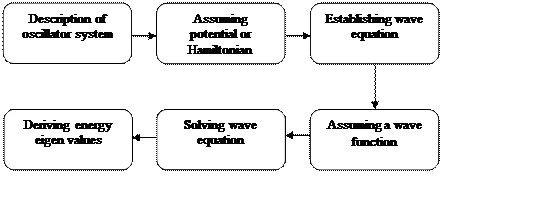
Figure 1. Flow chart for evaluating eigen values
Initially, the system of harmonic oscillator is described by considering various aspects. Under classical case, these conditions can be employed to determine potential of the system. However, a Hamiltonian is to be calculated if the system is in quantum state. The Hamiltonian is required if kinetic and potential energies are known. The assumed potential is utilized to setup a wave equation of second order. But, to solve such equations, it is a need to select some wave function which is based on the parameters required to evaluate. The result obtained by solving these equations is the eigen energy values of harmonic oscillator. These values are utilized for further solving the complex problems in which harmonic oscillators are to be used. The block diagram for various methods considered in this paper to solve harmonic oscillator problem in 1-D is shown in Fig. 2.
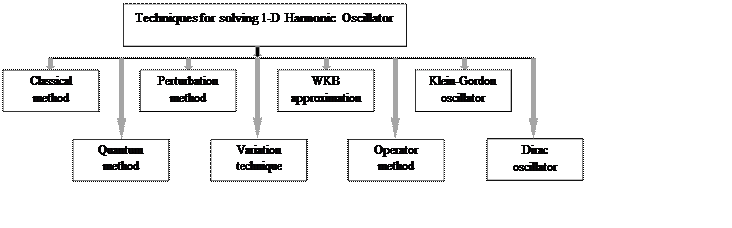
Figure 2. Block diagram for different techniques to solve the Harmonic oscillator
i. Linear Harmonic oscillator by classical mechanics
The 1-D Linear Harmonic Oscillator (LHO) consists of a particle of mass m which is bound to an equilibrium position x = 0 by a restoring force, F, proportional to the displacement x from mean position
i.e.![]()
where ‘k’ is the force constant.
The potential energy V(x) of an oscillator will be,
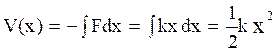
Also, the kinetic ener gy of an oscillator is,
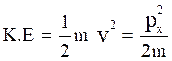
where ‘v’ and ‘p’ referes to velocity and linear momentum of the oscillator.
Thus, its total energy is represented by,
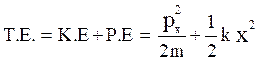 (1)
(1)
By Wilson-Sommerfeld quantization rule, we have,
![]() (2)
(2)
It is obvious that the particle undergoes a SHM in 1-D which is represented by a closed curve in phase space having two coordinates x and px
i.e.
![]() (3)
(3)
where, a is a semi major axis and b is a semi minor axis in phase space (x, p x).
If p x = 0, x = a then eq. (1) becomes,
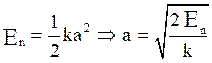
If p x = b, x = 0 then eq. (1) becomes,
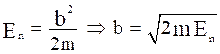
Also, eq.(2) becomes,
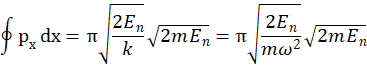
i.e.
![]() (4)
(4)
wherein w = 2pn is the angular frequency of the oscillator, oscillating with a frequency of n. On comparing eq.(2) and (4), we get,
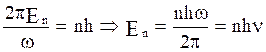
i.e. ![]() (5)
(5)
Eq. (5) is the classical result, while quantum mechanically the energy levels of harmonic oscillator are not continuous but, an integral multiple of hν; h being the Planck’s constant.
ii. LHO by Schrodinger time independent equation and Hermite polynomials with recursion formula
Consider, the two atoms of some masses joined together by an interaction force between them which results in the system executing harmonic oscillations with a restoring force. The potential energy between the two atoms is shown in Fig. 1.
At k = a, the potential energy is minimum and is represented as,
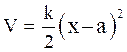
In case of a LHO, it is possible to represent the force as F = - kx by a potential energy as,
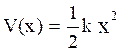
Let, a particle of mass is undergoing SHO with amplitude a then the displacement from origin at time t will be,
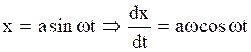
i.e. 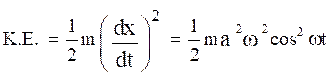
i.e. 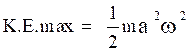
or K.E. max = K.E.+P.E
i.e.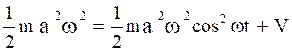
i.e. 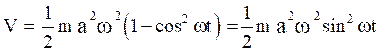
i.e. 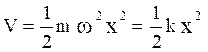
Thus, the Schrodinger time independent equation will be,
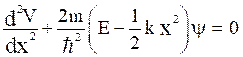 (6)
(6)
where ![]() and y is the wave function.
and y is the wave function.
Let, ![]() be a solution of the above equation.
be a solution of the above equation.
Thus, we have,
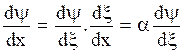 and
and
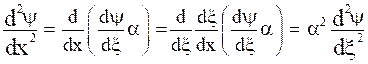
Thus, eq. (6) becomes,
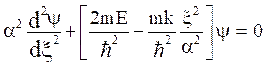
i.e. 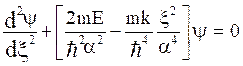 (7)
(7)
Let, α is chosen such that,
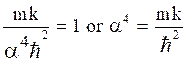
i.e. 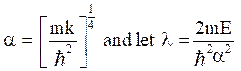
or 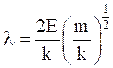 (8)
(8)
Thus, eq. (7) becomes,
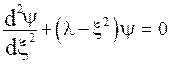 (9)
(9)
Let, ![]() (10)
(10)
is a solution of eq.(8) in which H(ξ) represents a polynomial of finite order in ξ.
Differentiating eq. (10) to second order and solving eq. (8), we get,
![]()
Eq. (10) can be solved to obtain a recursion formula as,
where, v represents any integer with a0 as energy level of ground state. The value of any index S may be 0 or 1 and it is possible to express λ in terms of any quantum number n as, λ = 2n+1
i.e. 
i.e. 
For n=0, we have,
is called as a zero point energy. From above equation, it is proved that all the energy levels get shifted by an amount equal to half of the separation of energy levels.
iii. Perturbed Harmonic Oscillator:
Let, the wave function of the system with perturbation theory is represented as,
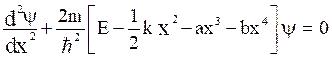 (11)
(11)
If the values of a and b are zero then the wave equation is for harmonic oscillator. If the values of a and b are small, then these terms are perturbed.
i.e. ![]() (12)
(12)
We know that, the first order perturbation energy is given by,
![]()
i.e. 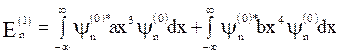
i.e. 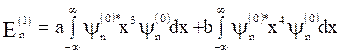 (13)
(13)
As the term x3 is an odd and ![]()
![]() is an even then the first term of eq.(13)
will be zero i.e. the first order perturbation due to
is an even then the first term of eq.(13)
will be zero i.e. the first order perturbation due to ![]() is zero
is zero
i.e. 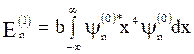 (14)
(14)
Let, 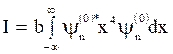 (15)
(15)
For a linear harmonic oscillator, we have,
![]() (16)
(16)
Thus, eq. (14) becomes,
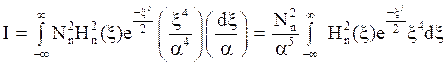 (17)
(17)
Solving above equation, we get,
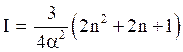
Thus, eq. (14) becomes,
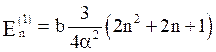 (18)
(18)
The total energy of the first order will be,
![]()
i.e. 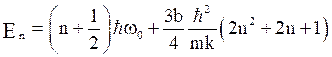 for
for 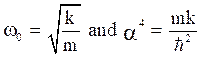
This is an eigen energy value which consists of an additional second term arises due to a perturbed system.
iv. Harmonic oscillator by variation method
Consider, the ground state of harmonic oscillator with Hamiltonian operator given by,
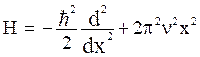 for
x is over a range of
for
x is over a range of ![]() .
.
Consider, any function Ψ obeys the condition given by,
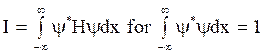
The normalization condition for Ψ means that it is an even function.
Let, ![]() for some constant A and α is a particle.
for some constant A and α is a particle.
Thus,
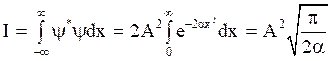 (19)
(19)
Also, 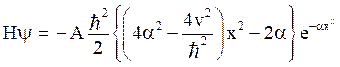
Thus,
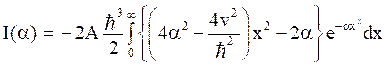 (20)
(20)
Integrating by parts, we get,
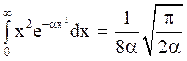
Thus, eq. (19) and (20) gives,
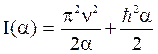 (21)
(21)
But, the condition 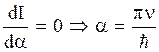
Thus,
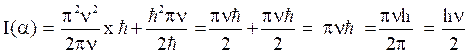
is the lowest energy and which equivalent to zero point energy of the quantum harmonic oscillator.
The required function is represented as,
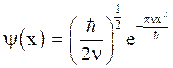
v. Harmonic oscillator by the Wentzel–Kramers–Brillouin (WKB) approximation method
The energy levels can be determined by Bohr’s rule of quantization given by,
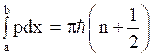 for
n is an integer and p is a momentum represented by,
for
n is an integer and p is a momentum represented by,
![]()
Here, 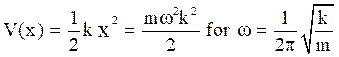 is a classical frequency, a and b are turning
points of an oscillator and kinetic energy at the extremities will be
is a classical frequency, a and b are turning
points of an oscillator and kinetic energy at the extremities will be
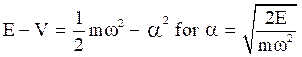
The turning points are 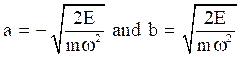
Thus, we have,
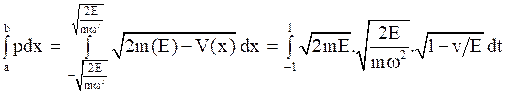
Assume that 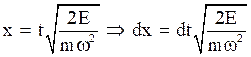
Thus, 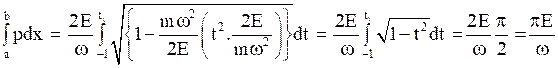
which results in
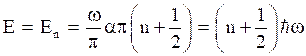
is the required eigen energy levels which also consists of zero point energy for n=0.
vi. Klein-Gordon oscillator
The relativistic oscillators are significant having special features when oscillator motion becomes relativistic. Increase in relativistic mass, oscillator becomes more sluggish with frequency and energy level spacing decrease.
The 1-D Klein-Gordon equation for a vector potential is given by,
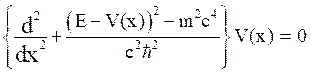 (22)
(22)
In Schrodinger wave equation, we have,
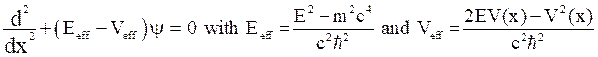
When the harmonic oscillator potential is stated by 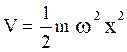 is introduced, then
effective potential takes the form,
is introduced, then
effective potential takes the form,
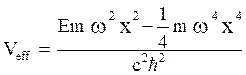 (23)
(23)
The 1-D free particle Klein-Gordon equation 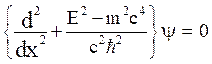 is represented as,
is represented as,
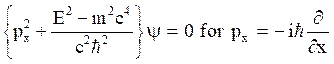 (24)
(24)
A new type of interaction in Klein-Gordon equation with linear momentum as
![]()
Let, ![]()
Thus, eq. (24) becomes,
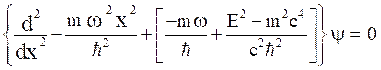 (25)
(25)
The resulting Klein-Gordon equation reduces to non-relativistic harmonic oscillator problem and hence is called as Klein-Gordon oscillator.
Let, 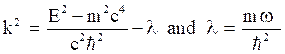
Thus, eq. (25) becomes,
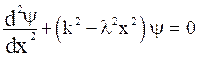 (26)
(26)
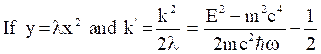
Then eq. (26) becomes,
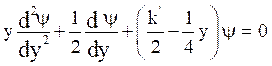 (27)
(27)
![]()
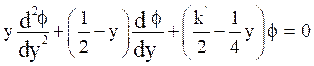 (28)
(28)
This equation is equivalent to Schrodinger equation with usual harmonic oscillator potential. The eigen functions are expressed in terms of hyper geometric functions m(a,c,y) as,
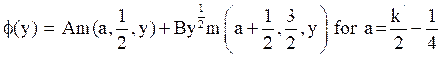
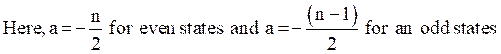 .
.
The eigen energies of 1-D Klein-Gordon oscillator is given by,
![]()
![]()
which is in relativistic form and is vary much different as compared to that of quantum mechanical eigen value.
vii. 1-D Dirac oscillator
The Dirac equation for a free particle in one dimension is given by,
![]() (29)
(29)
where, ![]() and
and ![]() are standard Dirac
matrices.
are standard Dirac
matrices.
The 1-D Dirac equation with oscillator potential is,
![]() (30)
(30)
i.e. 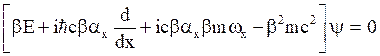 (31)
(31)
The values of ![]() and
and ![]() in terms of Pauli matrices are,
in terms of Pauli matrices are,
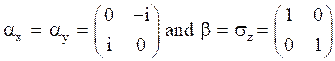
Eq.(31) in matrix form will be,
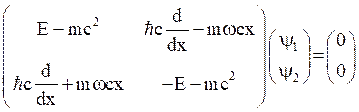 (32)
(32)
The coupled differential equation will be,
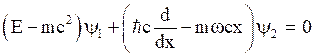 (33)
(33)
and 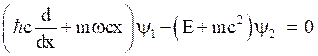 (34)
(34)
Using eq. (34) in eq.(33), we get,
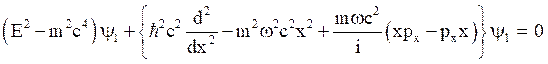 (35)
(35)
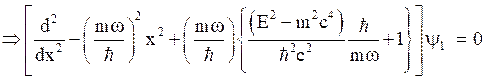 (36)
(36)
where, ![]() is
used.
is
used.
By eliminating ![]() from eq.(6), the eq.(8) becomes,
from eq.(6), the eq.(8) becomes,
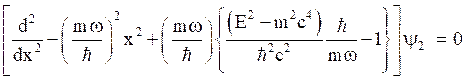 (37)
(37)
Eq.(36) and eq.(37) are Dirac equations for an oscillator potential for spin up and spin down states.
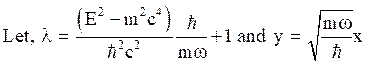
Thus, eq.(36) becomes,
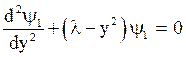 (38)
(38)
But for linear harmonic oscillator,
![]()
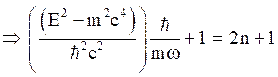
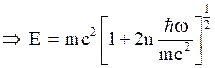 (39)
(39)
i.e. 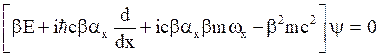 (40)
(40)
The values of ![]() and
and ![]() in terms of Pauli matrices are,
in terms of Pauli matrices are,
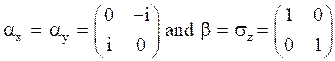
Eq. (40) in matrix form will be,
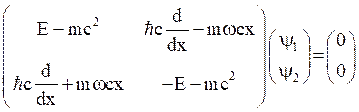 (41)
(41)
The coupled differential equations will be,
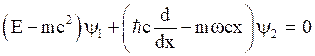 (42)
(42)
and
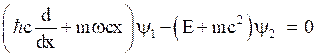 (43)
(43)
Using eq. (43) in (42), we get,
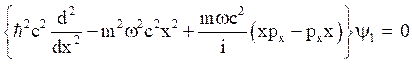 (44)
(44)
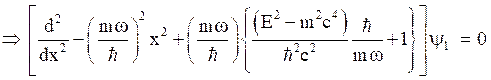 (45)
(45)
where, ![]() is
used.
is
used.
By eliminating ![]() from eq. (43), eq.(45) becomes,
from eq. (43), eq.(45) becomes,
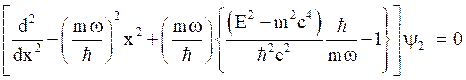 (46)
(46)
Eq. (45) and (46) are Dirac equations for an oscillator potential for spin-up and spin down states.
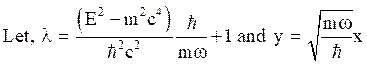 in eq.(45), we
get,
in eq.(45), we
get,
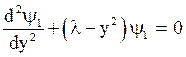 (47)
(47)
By the definition of linear harmonic oscillator, we have,
![]()
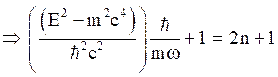
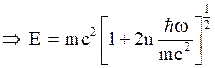 for spin up
states.
for spin up
states.
Solving eq. (46) for spin down states, the eigen energies will be,
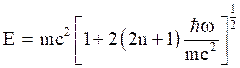
which is of the relativistic form and eigen energy of Dirac oscillator is said to be in complex form and is very difficult to determine it.
viii. Ladder operator method
The generalized harmonic oscillator forms the basis for explaining the concepts in quantum mechanics such as theory of radiation, vibrations of atoms in crystal lattice etc. The generalized Hamiltonian of the problem is given as,
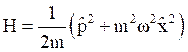 (48)
(48)
where, m is mass of an oscillating particle, ω is an angular frequency of vibration i.e. ω =2πυ, υ is a classical frequency. Here, p and x are momentum and position operators respectively.
The eigen value equation for the system is
![]() (49)
(49)
where, E is an energy eigen value which is to be calculated. The method employed in this article is to calculate the eigen vectors and operator matrices by using algebraic manipulations of ladder operators and the harmonic oscillator is quantized based on the operators which obeys the modified commutation rule represented as,
![]()
where, ![]() for β is any
positive constant.
for β is any
positive constant.
In addition to momentum
and position operators, for making calculations in matrix form it is convenient
to use the creation and annihilation operators![]() and
and ![]() given as,
given as,
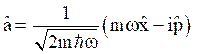 (50)
(50)
and 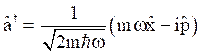 (51)
(51)
Here ![]() is an adjoint of
is an adjoint of![]() .
.
On multiplying equation (3) by (4) from right and simplifying, we get,
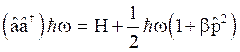 (52)
(52)
Similarly, on multiplying eq.(4) by (3) from left,
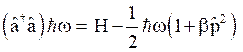 (53)
(53)
On comparing and solving eq. (5) and (6),
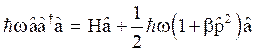 (54)
(54)
Readjusting eq. (52), we get,
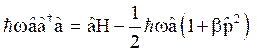 (55)
(55)
Also modifying eq. (53),
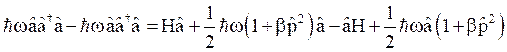
On solving eq. (54) and (55),
![]()
i.e. ![]() (56)
(56)
Similarly,
![]() (57)
(57)
But, in general the vector product yields the square of these vectors in magnitude as,
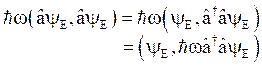
i.e. 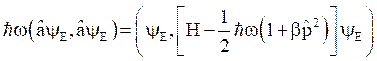
i.e. 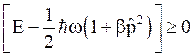
i.e. 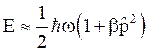
This is the lowest value of the energy of an oscillator. It consists of an additional bracket term along with the zero point energy.
Equations summary
The results obtained for energy eigen values for 1-D harmonic oscillator through various methods are summarized in the Table 1.
Table 1. Eigen values of Harmonic oscillators with various techniques
|
Sr. No. |
Methods of solving 1-D harmonic oscillator |
Energy eigen values |
|
1 |
Classical mechanics |
|
|
2 |
Schrodinger time independent equation |
|
|
3 |
Perturbation theory |
|
|
4 |
Variation method |
|
|
5 |
WKB approximation method |
|
|
6 |
Klein-Gordon oscillator (Relativistic) |
|
|
7 |
Dirac oscillator |
|
|
8 |
Ladder operator method |
|
References